2022-2023学年天津市滨海新区高一（下）期末数学试卷

一、选择题：本卷共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的，请将所选答案填入答题纸中的答题栏内．

• 1．化简

  AC

  -

  AB

  +

  CB

  =（　　）

  A． 2 CB

  B． 2 BC

  C． 2 AB

  D． 0
  组卷：170引用：2难度：0.8

  解析

• 2．若一组数据为35，42，42，66，72，79，85，86，88，则这组数据的极差为（　　）

  A．72

  B．66

  C．53

  D．42
  组卷：95引用：2难度：0.8

  解析

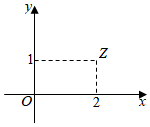• 3．在复平面内，复数z对应的点Z如图所示，则复数

  z

  =（　　）

  A．2+i

  B．2-i

  C．1+2i

  D．1-2i
  组卷：237引用：5难度：0.9

  解析

• 4．从一个容量为100的总体中抽取容量为10的样本，选取简单随机抽样和分层随机抽样两种不同方法抽取样本．在简单随机抽样中，总体中每个个体被抽中的概率为p₁，某个体第一次被抽中的概率为p₂；在分层随机抽样中，总体中每个个体被抽中的概率为p₃，则（　　）

  A．p2＜p1＜p3	B．p1=p2=p3
  C．p2＜p1=p3	D．p1，p2，p3之间没有关系
  组卷：148引用：1难度：0.8

  解析

• 5．甲、乙两台机床同时生产一种零件，在10天中，两台机床每天生产的次品数分别为：
  

  甲	2	3	1	1	0	2	1	1	0	1
  乙	0	1	0	2	2	0	3	1	2	4

  记甲、乙两台机床在这10天中生产次品数的平均数分别为

  x

  甲

  ，

  x

  乙

  ，方差分别为

  S

  2

  甲

  ，

  S

  2

  乙

  则下列说法正确的是（　　）

  A． x 甲 ＞ x 乙 ， S 2 甲 ＞ S 2 乙	B． x 甲 ＞ x 乙 ， S 2 甲 ＜ S 2 乙
  C． x 甲 ＜ x 乙 ， S 2 甲 ＞ S 2 乙	D． x 甲 ＜ x 乙 ， S 2 甲 ＜ S 2 乙
  组卷：119引用：2难度：0.8

  解析

• 6．已知向量

  a

  =

  （

  3

  ，-

  1

  ）

  ，

  b

  =

  （

  m

  ,

  1

  ）

  ．若向量

  a

  -

  b

  与

  b

  平行，则m=（　　）

  A．-3

  B．1

  C．1或2

  D．2
  组卷：149引用：3难度：0.8

  解析

• 7．已知一个圆锥的底面半径为2，其侧面积是底面积的2倍，则该圆锥的体积为（　　）

  A． 8 π 3

  B． 8 3 π 3

  C．8π

  D． 8 3 π
  组卷：197引用：2难度：0.8

  解析

• 8．已知α，β是两个不同的平面，l,m是两条不同的直线，则下列说法正确的是（　　）

  A．若l∥α，α∥β，则l∥β

  B．若α⊥β，α∩β=l,m⊥l,则m⊥β

  C．若l∥α，m⊂α，则l∥m

  D．若l⊥α，m⊥α，则l∥m
  组卷：137引用：2难度：0.7

  解析

三、解答题：本大题共4小题，共50分．解答应写出文字说明，证明过程或演算步骤．

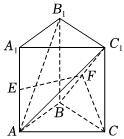• 23．如图，在直三棱柱ABC-A₁B₁C₁中，AB⊥BC，AB=BC=CC₁=1，E为AA₁的中点，F为BC₁的中点．
  （1）求证：EF∥平面ABC；
  （2）求证：CF⊥平面ABC₁；
  （3）求直线A₁C₁与平面ABC₁所成的角．
  组卷：418引用：2难度：0.5

  解析

• 24．在△ABC中，内角A，B，C的对边分别为a,b,c,已知sinA=sinB+sin（C-B）．
  （1）求角C的值；
  （2）若a＞b,且△ABC的面积

  S

  =

  3

  6

  c

  2

  ．
  （i）求证：

  c

  =

  3

  b

  ；
  （ii）已知点E在AB上，且满足

  CA

  +

  1

  2

  CB

  =

  λ

  CE

  ，延长CE到D，使得

  CD

  =

  2

  CE

  ，连接AD，BD，求cos∠ADB．
  组卷：148引用：3难度：0.4

  解析