2022-2023学年天津市河北区高一(下)期末数学试卷
发布:2024/5/26 8:0:9
一、选择题:本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.下列事件中,是随机事件的是( )
①明天本市会下雨;
②投掷2颗质地均匀的骰子,点数之和为14;
③抛掷一枚质地均匀的硬币,字朝上;
④13个人中至少有2个人的生日在同一个月.组卷:403引用:2难度:0.8 -
2.i是虚数单位,若(2k2-3k-2)+(k2-2k)i是纯虚数,则实数k的值为( )
组卷:185引用:2难度:0.9 -
3.已知向量
,a=(-1,4),若b=(3,-2λ),则λ=( )a∥(2a+b)组卷:341引用:8难度:0.7 -
4.若一个圆锥的底面半径为2,母线长为3,则该圆锥的侧面积为( )
组卷:194引用:1难度:0.7 -
5.如图,已知△ABC中,D为AB的中点,
,若AE=13AC,则λ+μ=( )DE=λAB+μBC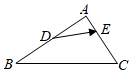 组卷:1024引用:14难度:0.9
组卷:1024引用:14难度:0.9 -
 6.设A、B、C、D是某长方体四条棱的中点,则直线AB和直线CD的位置关系是( )组卷:201引用:3难度:0.5
6.设A、B、C、D是某长方体四条棱的中点,则直线AB和直线CD的位置关系是( )组卷:201引用:3难度:0.5
三、解答题:本大题共4个小题,共40分.解答应写出文字说明、证明过程或演算步骤.
-
 18.某学校有学生1000人,为了解学生对本校食堂服务满意程度,随机抽取了100名学生对本校食堂服务满意程度打分,根据这100名学生的打分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
18.某学校有学生1000人,为了解学生对本校食堂服务满意程度,随机抽取了100名学生对本校食堂服务满意程度打分,根据这100名学生的打分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求频率分布直方图中a的值,并估计该校学生满意度打分不低于70分的人数;
(2)试估计该校学生满意度打分的众数、中位数(中位数保留小数点后2位);
(3)若采用分层随机抽样的方法,从打分在[40,60)的学生中随机抽取5人了解情况,再从中选取2人进行跟踪分析,求这2人打分都在[50,60)的概率.组卷:151引用:2难度:0.5 -
 19.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,AB=2,∠BAD=60°,M是PD的中点.
19.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,AB=2,∠BAD=60°,M是PD的中点.
(Ⅰ)求证:OM∥平面PAB;
(Ⅱ)平面PBD⊥平面PAC;
(Ⅲ)当三棱锥C-PBD的体积等于时,求PA的长.32组卷:712引用:5难度:0.7


