2023年北京大学附中高考数学三模试卷

一、选择题共10小题，每小题4分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.

• 1．已知集合P={x|x²≤4}，M={m}，若P∩M=M，则m的取值范围是（　　）

  A．（-∞，-2]	B．[-2，2]
  C．[2，+∞）	D．（-∞，-2]∪[2，+∞）
  组卷：635引用：5难度：0.7

  解析

• 2．抛物线y²=8x的焦点到准线的距离是（　　）

  A．1

  B．2

  C．4

  D．8
  组卷：647引用：57难度：0.9

  解析

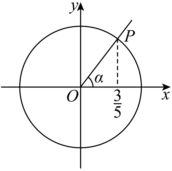• 3．如图，点P为角α的终边与单位圆O的交点，tan（α+π）=（　　）

  A． - 3 4

  B． 3 4

  C． - 4 3

  D． 4 3
  组卷：272引用：3难度：0.7

  解析

• 4．在

  （

  x

  +

  2

  x

  ）

  3

  的展开式中，常数项为（　　）

  A．1

  B．3

  C．6

  D．12
  组卷：137引用：2难度：0.7

  解析

• 5．现从3名男同学和2名女同学中选取两人加入“数学兴趣小组”，用A表示事件“抽到两名同学性别相同”，B表示事件“抽到两名女同学”，则在已知A事件发生的情况下B事件发生的概率即P（B|A）=（　　）

  A． 1 4

  B． 1 3

  C． 2 5

  D． 1 2
  组卷：585引用：7难度：0.7

  解析

• 6．已知圆O：x²+y²=1，直线3x+4y-10=0上动点P，过点P作圆O的一条切线，切点为A，则|PA|的最小值为（　　）

  A．1

  B． 2

  C． 3

  D．2
  组卷：1206引用：11难度：0.8

  解析

• 7．将函数y=sin2x的图象向左平移φ（φ＞0）个单位，得到的图象恰好关于直线x=

  π

  6

  对称，则φ的最小值是（　　）

  A． π 12

  B． π 6

  C． π 4

  D． π 3
  组卷：417引用：6难度：0.7

  解析

三、解答题共6题，共85分.解答应写出文字说明、演算步骤或证明过程.

• 20．已知函数f（x）=e^ax（x-1）²．
  （1）若a=1，求f（x）在（0，f（0））处切线方程；
  （2）求f（x）的极大值与极小值；
  （3）证明：存在实数M，当a＞0时，函数y=f（x）-M有三个零点．
  组卷：459引用：7难度：0.5

  解析

• 21．已知A为有限个实数构成的非空集合，设A+A={a_i+a_j|a_i，a_j∈A}，A-A={a_i-a_j|a_i，a_j∈A}，记集合A+A和A-A其元素个数分别为|A+A|，|A-A|．
  设n（A）=|A+A|-|A-A|．例如当A={1，2}时，A+A={2，3，4}，A-A={-1，0，1}，|A+A|=|A-A|，所以n（A）=0．
  （1）若A={1，3，5}，求n（A）的值；
  （2）设A是由3个正实数组成的集合且（A+A）∩A=∅，A′=A∪{0}，证明：n（A′）-n（A）为定值；
  （3）若{a_n}是一个各项互不相同的无穷递增正整数数列，对任意n∈N^*，设A_n={a₁，a₂，…，a_n}，b_n=n（A_n）．已知a₁=1，a₂=2，且对任意n∈N^*，b_n≥0，求数列{a_n}的通项公式．
  组卷：234引用：5难度：0.3

  解析