当前位置：试卷中心 > 试卷详情

2023-2024学年重庆市万州二中教育集团高二（上）月考数学试卷（10月份）

发布：2024/9/6 16:0:9

1．直线
x
+
3
y
+
5
=
0
的倾斜角是（　　）
A．30° B．120° C．60° D．150°
组卷：287引用：26难度：0.9
解析
2．已知
AB
=（2，3，1），
AC
=（4，5，3），那么向量
BC
=（　　）
A．（-2，-2，-2） B．（2，2，2） C．（6，8，4） D．（8，15，3）
组卷：481引用：4难度：0.8
解析
3．已知
{
a
，
b
，
c
}
是空间的一个基底，下列不能与
m
=
a
-
b
，
n
=
b
-
c
构成空间的另一个基底的是（　　）
A．
a
-
c
B．
a
+
c
C．
a
+
b
D．
a
+
b
+
c
组卷：156引用：3难度：0.9
解析
4．直线ax+2y+4=0与直线x+（a-1）y+2=0平行，则a的值为（　　）
A．a=2 B．a=0 C．a=-1 D．a=-1或a=2
组卷：580引用：14难度：0.8
解析
5．在正三棱锥P-ABC中，O是△ABC的中心，PA=AB=2，则
PO
•
PA
=（　　）
A．
5
9
B．
6
3
C．
4
2
3
D．
8
3
组卷：82引用：7难度：0.7
解析
6．已知直线l过点P（1，3，1），且方向向量为
m
=
（
1
，
0
，-
1
）
，则点A（1，-1，-1）到l的距离为（　　）
A．
3
2
B．4 C．
2
5
D．3
组卷：104引用：5难度：0.6
解析
7．已知A（3，0），B（0，3），从点P（0，2）射出的光线经x轴反射到直线AB上，又经过直线AB反射回到P点，则光线所经过的路程为（　　）
A．
2
10
B．6 C．
3
3
D．
26
组卷：1583引用：9难度：0.5
解析

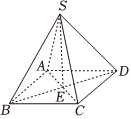21．在四棱锥S-ABCD中，已知底面ABCD为菱形，若BD⊥SC，AC⊥SD，BD∩AC=E．
（1）求证：SE⊥平面ABCD；
（2）若BD=
3
AC=2SE，设点H满足
DH
=μ
DC
（0＜μ＜1），当直线SC与平面SHE所成角的正弦值为
7
7
时，求μ的值．
组卷：146引用：3难度：0.6
解析
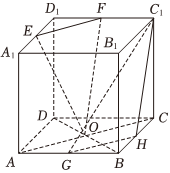22．如图，在正方体ABCD-A₁B₁C₁D₁中，E，F分别为A₁D₁，C₁D₁中点，G，H分别为AB，BC中点，O为平面ABCD中心，且正方体棱长为1．
（1）证明：平面OEF∥平面C₁GH；
（2）是否存在过直线EF且与正方体的12条棱的夹角均相等的平面？若存在，求出该平面与平面C₁GH的夹角的余弦值．
组卷：34引用：3难度：0.3
解析