2022-2023学年天津实验中学滨海学校高一(下)期中数学试卷
发布:2024/6/28 8:0:9
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.如图,向量
=AB,a=AC,b=CD,则向量c可以表示为( )BD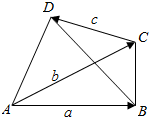 组卷:3288引用:31难度:0.9
组卷:3288引用:31难度:0.9 -
2.已知复数z在复平面上对应的点为(2,-1),则( )
组卷:197引用:5难度:0.8 -
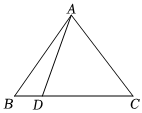 3.如图,若D点在三角形ABC的边BC上,且,CD=3DB,则x+2y的值为( )AD=xAB+yAC组卷:328引用:3难度:0.7
3.如图,若D点在三角形ABC的边BC上,且,CD=3DB,则x+2y的值为( )AD=xAB+yAC组卷:328引用:3难度:0.7 -
4.已知
,|a|=4且b=(-1,0),则(a+2b)⊥b与a的夹角为( )b组卷:239引用:4难度:0.8 -
5.设
是两个非零向量,则下列命题中错误的是( )a,b组卷:176引用:3难度:0.8 -
6.在△ABC中,已知
,且sinA=2sinBcosC,则△ABC是( )|AB+AC|=|AB-AC|组卷:197引用:7难度:0.8 -
7.已知点A(1,1),B(0,2),C(-1,-1).则
在AB上的投影向量为( )BC组卷:411引用:9难度:0.6 -
8.下列有五个命题:
①若直线a∥平面α,a∥平面β,α∩β=m则α∥m;
②若直线α∥平面α,则α与平面α内任何直线都平行;
③若直线α∥平面α,平面α∥平面β,则α∥平面β;
④如果a∥b,a∥平面α,那么b∥平面α;
⑤对于异面直线a、b存在唯一一对平面α、β使得a⊂平面α,b⊂平面β,且α∥β.
其中正确的个数是( )组卷:150引用:3难度:0.8
三、解答题:本大题共4小题,共50分.解答应写出文字说明,证明过程或演算步骤.
-
23.在△ABC中,角A,B,C所对的边分别为a,b,c,已知
.2c=a+cosAbcosB
(1)求角B的大小;
(2)若,求△ABC的面积.b=4,a+c=32组卷:374引用:8难度:0.6 -
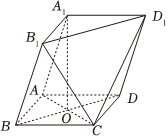 24.由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示,四边形ABCD为平行四边形,O为AC与BD的交点.
24.由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示,四边形ABCD为平行四边形,O为AC与BD的交点.
(1)求证:A1O∥平面B1CD1;
(2)求证:平面A1BD∥平面B1CD1;
(3)设平面B1CD1与底面ABCD的交线为l,求证:BD∥l.组卷:738引用:3难度:0.5


