2022-2023学年河北省邢台市高二(上)第一次月考数学试卷
发布:2024/7/25 8:0:9
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.直线x-y=0绕原点逆时针旋转90°后所对应的直线斜率为( )
组卷:333引用:4难度:0.7 -
2.已知空间三点A(3,2,0),B(3,2,2),C(3,0,1),则C到直线AB的距离为( )
组卷:86引用:10难度:0.7 -
3.已知直线l经过点(-1,4),且它的一个方向向量为
,则( )n=(-2,4)组卷:44引用:3难度:0.7 -
4.已知A(1,-2,1),B(1,-5,4),C(2,3,4),则
在AC上的投影向量为( )AB组卷:1192引用:9难度:0.8 -
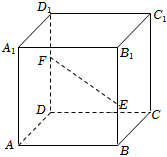 5.如图,在平行六面体ABCD-A1B1C1D1中,E,F分别在棱BB1和DD1上,且.记DF=12DD1,若EF=xAB+yAD+zAA1,则x+y+z=14=( )BEBB1组卷:109引用:9难度:0.8
5.如图,在平行六面体ABCD-A1B1C1D1中,E,F分别在棱BB1和DD1上,且.记DF=12DD1,若EF=xAB+yAD+zAA1,则x+y+z=14=( )BEBB1组卷:109引用:9难度:0.8 -
6.若直线l的斜率
,则直线l的倾斜角的取值范围是( )k∈[-1,33]组卷:390引用:13难度:0.8 -
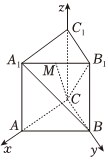 7.在直三棱柱ABC-A1B1C1中,CA=CB=2,∠BCA=90°,M是A1B1的中点,以C为坐标原点建立如图所示的空间直角坐标系C-xyz,若,则异面直线CM与A1B夹角的余弦值为( )A1B⊥CB1组卷:15引用:3难度:0.7
7.在直三棱柱ABC-A1B1C1中,CA=CB=2,∠BCA=90°,M是A1B1的中点,以C为坐标原点建立如图所示的空间直角坐标系C-xyz,若,则异面直线CM与A1B夹角的余弦值为( )A1B⊥CB1组卷:15引用:3难度:0.7
四、解答题:本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.
-
21.如图①,在平面多边形ABCDE中,
,△ADE为等腰直角三角形,四边形ABCD为等腰梯形,且AD∥BC,沿AD将△ADE折起,使得AB=AD=AE=12BC=1,M为BC的中点,连接AM,BD,如图②.BE=2
(1)证明:BD⊥EM.
(2)求直线DE与平面BEM所成角的正弦值.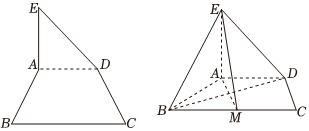 组卷:101引用:3难度:0.4
组卷:101引用:3难度:0.4 -
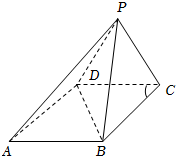 22.如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DCB=60°,AB⊥PB.
22.如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DCB=60°,AB⊥PB.
(1)证明:△PDC为等腰三角形;
(2)若平面PDC⊥平面ABCD,AB=2,求二面角A-PB-C的余弦值的取值范围.组卷:99引用:6难度:0.6


