2023年山西省运城中学高考数学二模试卷

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．已知R为实数集，全集U=R，集合A={x||x-1|＜2}，B={x|x≥1}，则∁_U（A∩B）=（　　）

  A．{x|-1≤x＜2}

  B．{x|x≤1或x＞3}

  C．{x|1≤x＜3}

  D．{x|x＜1或x≥3}
  组卷：327引用：4难度：0.7

  解析

• 2．已知i为虚数单位，若

  （

  3

  +

  i

  ）

  （

  a

  +

  2

  i

  ）

  1

  +

  i

  为实数，则实数a=（　　）

  A．-2

  B．4

  C．2

  D．-4
  组卷：78引用：6难度：0.8

  解析

• 3．函数f（x）=xe^x-2e^x+x+e在（1，f（1））处的切线方程为（　　）

  A．y=x

  B．y=2x-1

  C．y=ex-e+1

  D．y=-ex+e+1
  组卷：76引用：3难度：0.7

  解析

• 4．已知

  0

  ＜

  x

  1

  ＜

  x

  2

  ＜

  2

  π

  ，

  sin

  x

  1

  =

  sin

  x

  2

  =

  1

  3

  ，则cos（x₁-x₂）=（　　）

  A． 7 9

  B． - 7 9

  C． 7 3

  D． - 7 3
  组卷：131引用：5难度：0.7

  解析

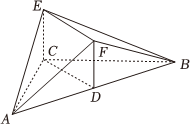• 5．风筝又称为“纸鸢”，由中国古代劳动人民发明于距今2000多年的东周春秋时期，相传墨翟以木头制成木鸟，研制三年而成，是人类最早的风筝起源．如图，是某高一年级学生制作的一个风筝模型的多面体ABCEF，D为AB的中点，四边形EFDC为矩形，且DF⊥AB，AC=BC=2，∠ACB=120°，当AE⊥BE时，多面体ABCEF的体积为（　　）

  A． 2 6 3

  B． 6 3

  C． 3 3

  D． 6
  组卷：226引用：6难度：0.5

  解析

• 6．已知F为抛物线C：y²=3x的焦点，过F的直线l交抛物线C于A，B两点，若|AF|=λ|BF|=λ，则λ=（　　）

  A．1

  B． 3 2

  C．3

  D．4
  组卷：164引用：4难度：0.5

  解析

• 7．已知△ABC是边长为2的等边三角形，M，N是△ABC边上的两个动点，若线段MN将△ABC分成面积相等的两部分，则线段MN长度的最小值为（　　）

  A． 3

  B． 3 2

  C． 2

  D．1
  组卷：111引用：5难度：0.5

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．已知点P（4，3）为双曲线

  E

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  上一点，E的左焦点F₁到一条渐近线的距离为

  3

  ．
  （1）求双曲线E的标准方程；
  （2）不过点P的直线y=kx+t与双曲线E交于A，B两点，若直线PA，PB的斜率和为1，证明：直线y=kx+t过定点，并求该定点的坐标．
  组卷：175引用：4难度：0.3

  解析

• 22．已知函数f（x）=x²+2cosx,f′（x）为函数f（x）的导函数．
  （1）讨论函数f（x）的单调性；
  （2）已知函数g（x）=f′（x）-5x+5alnx,存在g（x₁）=g（x₂）（x₁≠x₂），证明x₁+x₂＞2a.
  组卷：228引用：5难度：0.4

  解析