人教A版（2019）选择性必修第一册《第一章 空间向量与立体几何》2023年单元测试卷（9）

一、选择题

• 1．在空间直角坐标系中，

  a

  =

  （

  1

  ，

  2

  ，

  1

  ）

  为直线l的一个方向向量，

  n

  =

  （

  2

  ，

  t

  ,

  4

  ）

  为平面α的一个法向量，且l∥α，则t=（　　）

  A．3

  B．-3

  C．1

  D．-1
  组卷：725引用：18难度：0.8

  解析

• 2．两平行平面α，β分别经过坐标原点O和点A（2，1，1），且两平面的一个法向量

  n

  =（-1，0，1），则两平面间的距离是（　　）

  A． 3 2

  B． 2 2

  C． 3

  D．3 2
  组卷：464引用：17难度：0.7

  解析

• 3．在正四棱柱ABCD-A₁B₁C₁D₁中，AA₁=4，AB=BC=2，动点P，Q分别在线段C₁D，AC上，则线段PQ长度的最小值是（　　）

  A． 2 2 3

  B． 2 3 3

  C． 4 3

  D． 2 5 3
  组卷：190引用：8难度：0.4

  解析

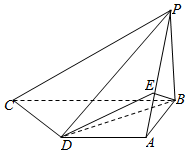• 4．如图，四棱锥P-ABCD中，PB⊥平面ABCD，底面ABCD为直角梯形，AD∥BC，AB⊥BC，AB=AD=PB=3，点E在棱PA上，且PE=2EA，则平面ABE与平面BED的夹角的余弦值为（　　）

  A． 2 3

  B． 6 6

  C． 3 3

  D． 6 3
  组卷：172引用：4难度：0.7

  解析

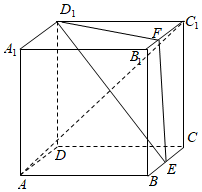• 5．正方体ABCD-A₁B₁C₁D₁的棱上到直线A₁B与CC₁的距离相等的点有4个，其中3个点分别为E，F，D₁，如图所示，则直线AC₁与平面EFD₁所成角的正弦值为（　　）

  A． 26 13

  B． 2 26 13

  C． 2 78 39

  D． 4 78 39
  组卷：35引用：6难度：0.4

  解析

四、解答题

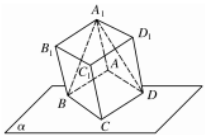• 15．如图，正方体ABCD-A₁B₁C₁D₁的顶点C在平面α上，所有顶点都在平面α的同一侧，且满足A₁B和A₁D与平面α所成角均为

  π

  3

  ．
  （Ⅰ）求证：BD∥平面α；
  （Ⅱ）求直线B₁D与平面α所成角的余弦值．
  组卷：127引用：2难度：0.8

  解析

• 16．四边形ABCD中，AB⊥AD，AD∥BC，AD=3，BC=2AB=2，E，F分别在BC，AD上，EF∥AB．现将四边形ABEF沿EF折起，使平面ABEF⊥平面EFDC．
  （Ⅰ）若BE=

  1

  2

  ，在折叠后的线段AD上是否存在一点P，且

  AP

  =

  λ

  PD

  ，使得CP∥平面ABEF？若存在，求出λ的值，若不存在，说明理由；
  （Ⅱ）求三棱锥A-CDF的体积的最大值，并求此时二面角E-AC-F的余弦值．
  组卷：72引用：2难度：0.3

  解析