2022-2023学年广东省梅州市丰顺县东联中学九年级（上）月考数学试卷（9月份）

一、选择题（共10题，共30分）

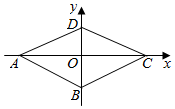• 1．如图，在平面直角坐标系内，四边形ABCD为菱形，点A，B的坐标分别为（-2，0），（0，-1），点C，D分别在坐标轴上，则菱形ABCD的周长等于（　　）

  A． 5

  B．4 3

  C．4 5

  D．20
  组卷：419引用：5难度：0.7

  解析

• 2．关于菱形的性质，以下说法不正确的是（　　）

  A．四条边相等	B．对角线互相垂直
  C．对角线相等	D．是轴对称图形
  组卷：885引用：32难度：0.5

  解析

• 3．小明在学习了正方形以后，给同桌小文出了道题：从下列四个条件：
  ①AB=BC；
  ②∠ABC=90°；
  ③AC=BD；
  ④AC⊥BD中选两个作为补充条件，使平行四边形ABCD为正方形．
  现有下列四种选法你认为错误的是（　　）

  A．①②

  B．①③

  C．②③

  D．②④
  组卷：450引用：6难度：0.5

  解析

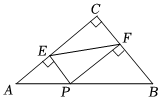• 4．如图，在△ABC中，∠C=90°，AC=8，BC=6，点P为斜边AB上一动点，过点P作PE⊥AC于E，PF⊥BC于点F，连接EF，则线段EF的最小值为（　　）

  A．24

  B．3.6

  C．4.8

  D．5
  组卷：3182引用：27难度：0.6

  解析

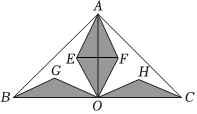• 5．四个形状大小相同的等腰三角形按如图所示方式摆放，已知∠AOB=∠AOC=90°，EF=2cm,若点F落在BG的延长线上，则图中阴影部分的面积为（　　）

  A． （ 4 2 + 4 ） c m 2

  B． （ 4 3 ） c m 2

  C． （ 2 2 + 8 ） c m 2

  D． （ 2 3 + 8 ） c m 2
  组卷：1552引用：7难度：0.3

  解析

• 6．《代数学》中记载，形如x²+10x=39的方程，求正数解的几何方法是：“如图1，先构造一个面积为x²的正方形，再以正方形的边长为一边向外构造四个面积为

  5

  2

  x的矩形，得到大正方形的面积为39+25=64，则该方程的正数解为8-5=3．”小聪按此方法解关于x的方程x²+6x+m=0时，构造出如图2所示的图形，已知阴影部分的面积为36，则该方程的正数解为（　　）
  

  A．6

  B．3 5 -3

  C．3 5 -2

  D．3 5 - 3 2
  组卷：2018引用：14难度：0.6

  解析

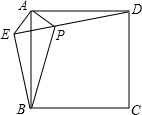• 7．已知：如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若AE=AP=1，PD=2，下列结论：①EB⊥ED；②∠AEB=135°；③S_{正方形ABCD}=5+2

  2

  ；④PB=2；其中正确结论的序号是（　　）

  A．①③④

  B．②③④

  C．①②④

  D．①②③
  组卷：637引用：3难度：0.4

  解析

• 8．菱形ABCD的边长是5，两条对角线交于O点，且AO，BO的长分别是关于x的方程x²+（2m-1）x+m²+3=0的根，则m的值为（　　）

  A．-3

  B．5

  C．5或-3

  D．-5或3
  组卷：933引用：10难度：0.7

  解析

三、解答题（共8小题，满分62分）

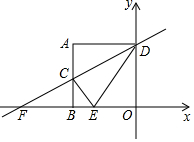• 24．如图，A（-2，2）、AB⊥x轴于点B，AD⊥y轴于点D，C（-2，1）为AB的中点，直线CD交x轴于点F．
  （1）求直线CD的函数关系式；
  （2）过点C作CE⊥DF且交x轴于点E，求证：∠ADC=∠EDC；
  （3）求点E坐标；
  （4）点P是直线CE上的一个动点，求PB+PF的最小值．
  组卷：1474引用：2难度：0.2

  解析

• 25．在平面直角坐标系中，四边形AOBC是矩形，点O（0，0），点A（5，0），点B（0，3）．以点A为中心，顺时针旋转矩形AOBC，得到矩形ADEF，点O，B，C的对应点分别为D，E，F．
  （Ⅰ）如图①，当点D落在BC边上时，求点D的坐标；
  （Ⅱ）如图②，当点D落在线段BE上时，AD与BC交于点H．
  ①求证△ADB≌△AOB；
  ②求点H的坐标．
  （Ⅲ）记K为矩形AOBC对角线的交点，S为△KDE的面积，求S的取值范围（直接写出结果即可）．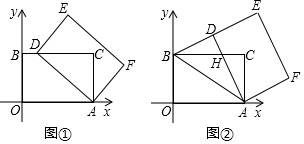
  
  组卷：5870引用：14难度：0.1

  解析