2023-2024学年河南省平许济洛高三(上)第一次质检数学试卷
发布:2024/9/20 9:0:9
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一个选项是符合题目要求的。
-
1.设全集U=R,集合A={y|y=2x},B={x|x2-3x+2<0},则A∩(∁UB)=( )
组卷:35引用:2难度:0.8 -
2.复数z满足i2023(2+z)=2-i,则
=( )z组卷:288引用:10难度:0.7 -
3.已知椭圆
的离心率为C:x2a2+y2b2=1(a>b>0)分别为C的左、右顶点,B为C的上顶点.若12,A1,A2,则椭圆C的方程为( )BA1•BA2=-2组卷:352引用:3难度:0.5 -
4.过圆x2+y2=4内点P(1,1)有若干条弦,它们的长度构成公差为d的等差数列{an},且
,其中a1,an分别为过点P的圆的最短弦长和最长弦长,则n的取值集合为( )d∈(16,13)组卷:37引用:2难度:0.5 -
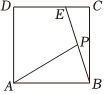 5.如图,正方形ABCD中,是线段BE上的动点,且DE=2EC,P,则AP=xAB+yAD(x>0,y>0)的最小值为( )1x+1y组卷:142引用:2难度:0.6
5.如图,正方形ABCD中,是线段BE上的动点,且DE=2EC,P,则AP=xAB+yAD(x>0,y>0)的最小值为( )1x+1y组卷:142引用:2难度:0.6 -
6.定义在R上的偶函数f(x)满足f(2-x)+f(x)=0,且f(x)在[-2,0]上单调递增.若
,则( )a=f(tan5π18),b=f(3),c=f(log43)组卷:41引用:3难度:0.6 -
7.2023贺岁档电影精彩纷呈,小明期待去影院观看.小明家附近有甲、乙两家影院,小明第一天去甲、乙两家影院观影的概率分别为
和25.如果他第一天去甲影院,那么第二天去甲影院的概率为35;如果他第一天去乙影院,那么第二天去甲影院的概率为35.若小明第二天去了甲影院,则第一天去乙影院的概率为( )12组卷:119引用:3难度:0.6
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
-
21.已知函数
.f(x)=x-lnx+m,g(x)=xex
(1)若函数f(x)和g(x)的图象都与平行于x轴的同一条直线相切,求m的值;
(2)若函数F(x)=f(x)-g(x)有两个零点x1,x2,证明:.ex1•ex2>e2组卷:47引用:2难度:0.4 -
22.已知抛物线C:x2=-4y,直线l垂直于y轴,与C交于M,N两点,O为坐标原点,过点N且平行于y轴的直线与直线OM交于点P,记动点P的轨迹为曲线E.
(1)求曲线E的方程;
(2)点A在直线y=-1上运动,过点A作曲线E的两条切线,切点分别为P1,P2,在平面内是否存在定点B,使得AB⊥P1P2?若存在,请求出定点B的坐标;若不存在,请说明理由.组卷:86引用:2难度:0.2


