2022-2023学年四川省眉山市仁寿一中南校区高二（上）月考数学试卷（文科）（12月份）

一、选择题：本题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．设命题p：∃x₀∈R，x₀²+1=0，则命题p的否定为（　　）

  A．∀x∉R，x2+1=0	B．∀x∈R，x2+1≠0
  C．∃x0∉R，x02+1=0	D．∃x0∈R，x02+1≠0
  组卷：253引用：14难度：0.8

  解析

• 2．已知两圆分别为圆C₁：x²+y²=49和圆C₂：x²+y²-6x-8y+9=0，这两圆的位置关系是（　　）

  A．相离

  B．外切

  C．内含

  D．相交
  组卷：140引用：6难度：0.8

  解析

• 3．下列条件中，能得到平面α∥平面β的条件是（　　）

  A．存在一条直线 a,a∥α，a∥β

  B．存在一条直线 a,a⊂α，a∥β

  C．存在两条平行直线 a,b,a⊂α，b⊂β，a∥β，b∥α

  D．存在两条异面直线 a,b,a⊂α，b⊂β，a∥β，b∥α
  组卷：148引用：6难度：0.7

  解析

• 4．已知抛物线C：y²=2px（p＞0）的焦点为F，过点（p,0）且垂直于x轴的直线与抛物线C在第一象限内的交点为A，若|AF|=1，则抛物线C的方程为（　　）

  A． y 2 = 4 3 x

  B．y2=2x

  C．y2=3x

  D．y2=4x
  组卷：171引用：3难度：0.7

  解析

• 5．设F₁，F₂是双曲线C：x²-

  y

  2

  3

  =1的左，右焦点，点P在双曲线C的右支上，当|PF₁|=6时，△PF₁F₂的面积为（　　）

  A．4 3

  B．3 7

  C． 455 2

  D．6 7
  组卷：146引用：6难度：0.7

  解析

• 6．已知一个圆锥的体积为3π，其侧面积是底面积的2倍，则其底面半径为（　　）

  A． 2 3

  B．3

  C． 3

  D． 3 3
  组卷：208引用：12难度：0.7

  解析

• 7．在正方体ABCD-A₁B₁C₁D₁中，E、F分别是A₁B₁、B₁C₁的中点，则异面直线AE与BF所成角的余弦值为（　　）

  A． 4 5

  B． 12 13

  C． 3 5

  D． 5 13
  组卷：52引用：2难度：0.6

  解析

三、解答题：解答应写出文字说明，证明过程或演算步骤.

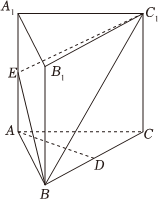• 21．如图，在正三棱柱ABC-A₁B₁C₁（底面为正三角形的直棱柱）中，AB=CC₁=2，D为BC的中点，E为侧棱AA₁上的点．
  （1）当E为AA₁的中点时，求证：AD∥平面BC₁E；
  （2）是否存在点E，使得三棱柱被平面BC₁E分成的上下两部分体积关系为

  V

  上

  V

  下

  =

  4

  5

  ，若存在，求AE的长，若不存在，说明理由．
  组卷：0引用：2难度：0.5

  解析

• 22．已知椭圆Γ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的离心率为

  6

  3

  ，左、右焦点分别为F₁，F₂，过F₂作不平行于坐标轴的直线交Γ于A，B两点，且△ABF₁的周长为

  4

  6

  ．
  （1）求Γ的方程；
  （2）求△ABF₁面积的取值范围；
  （3）若AM⊥x轴于点M，BN⊥x轴于点N，直线AN与BM交于点C，求证：点C在一条定直线上，并求此定直线．
  组卷：17引用：2难度：0.5

  解析