2023-2024学年浙江省绍兴市柯桥区联盟校八年级（上）月考数学试卷（10月份）
发布：2024/9/6 1:0:8
一.选择题（20分）
-
1．如图，下列图案是我国几家银行的标志，其中不是轴对称图形的是（ ）
组卷：265引用：15难度：0.9 -
2．下列各组长度的三条线段能组成三角形的是（ ）
组卷：275引用：8难度：0.7 -
3．下列选项中，可以用来说明命题“两个锐角的和是锐角”是假命题的反例是（ ）
组卷：195引用：10难度：0.7 -
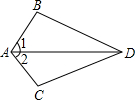4．如图，∠1=∠2，下列条件中不能使△ABD≌△ACD的是（ ）组卷：1480引用：15难度：0.5 -
5．如图，有一池塘，要测池塘两端A，B的距离，可先在平地上取一个直接到达A和B的点C，连接AC并延长到D，使CD=CA，连接BC并延长到E，使CE=CB，连接DE，那么量出DE的长，就是A、B的距离．我们可以证明出△ABC≌△DEC，进而得出AB=DE，那么判定△ABC和△DEC全等的依据是（ ）组卷：1792引用：18难度：0.9 -
6．如图，△ABC与△A′B′C′关于直线l对称，且∠A=105°，∠C′=30°，则∠B=（ ）组卷：1893引用：32难度：0.9 -
7．已知等腰的底边BC=8cm,且|AC-BC|=3cm,则腰AC的长为（ ）
组卷：211引用：3难度：0.7 -
8．在如图的方格中，△ABC的顶点A、B、C都是方格线的交点，则三角形ABC的外角∠ACD的度数等于（ ）组卷：316引用：7难度：0.9 -
9．如图，在△ABC中，BC＞AB＞AC．甲、乙两人想在BC上取一点P，使得∠APC=2∠ABC，其作法如下：
（甲）作AB的中垂线，交BC于P点，则P即为所求；
（乙）以B为圆心，AB长为半径画弧，交BC于P点，则P即为所求．
对于两人的作法，下列判断何者正确？（ ）组卷：287引用：7难度：0.9
三、解答题（6+6+6+6+8+8+10）
-
26．在△ABC中，BD平分∠ABC交AC于点D，点E是线段AC上的动点（不与点D重合），过点E作EF∥BC交射线BD于点F，∠CEF的角平分线所在直线与射线BD交于点G．
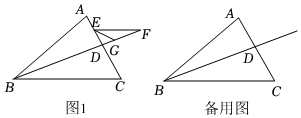
（1）如图1，点E在线段AD上运动．
①若∠ABC=40°，∠C=70°，则∠BGE=°；
②若∠A=50°，则∠BGE=°；
③探究∠BGE与∠A之间的数量关系，并说明理由；
（2）若点E在线段DC上运动时，直接写出∠BGE与∠A之间的数量关系．组卷：522引用：2难度：0.5 -
27．如图1，在△ABC中，AB=AC，D为射线BC上（不与B、C重合）一动点，在AD的右侧射线BC的上方作△ADE，使得AD=AE，∠DAE=∠BAC，连接CE．
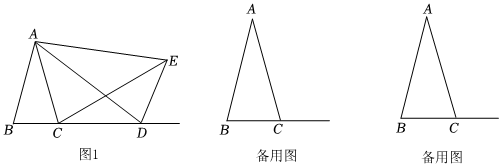
（1）找出图中的一对全等三角形，并证明你的结论；
（2）延长EC交AB的延长线于点F，若∠F=45°，
①利用（1）中的结论求出∠DCE的度数；
②当△ABD是等腰三角形时，直接写出∠ADB的度数；
（3）当D在线段BC上时，若线段BC=3，△ABC面积为3，则四边形ADCE周长的最小值是 ．组卷：570引用：2难度：0.2
