2023-2024学年浙江省杭州十三中教育集团九年级（上）月考数学试卷（10月份）

一.选择题（共10小题）

• 1．下列事件是随机事件的是（　　）

  A．a2+b2=-1（其中a,b都是实数）

  B．经过有信号灯的十字路口，遇见绿灯

  C．掷一枚骰子，向上一面的点数是7

  D．任意画一个三角形，其内角和是180°
  组卷：51引用：3难度：0.8

  解析

• 2．若抛物线y=-x²+bx+c经过点（-2，3），则c-2b的值是（　　）

  A．7

  B．-1

  C．-2

  D．3
  组卷：628引用：8难度：0.6

  解析

• 3．函数y=-2x²先向右平移3个单位，再向下平移7个单位，所得函数解析式是（　　）

  A．y=-2（x-3）2+7	B．y=-2（x-3）2-7
  C．y=-2（x+3）2+7	D．y=-2（x+3）2-7
  组卷：261引用：4难度：0.6

  解析

• 4．在平面直角坐标系中，以原点O为圆心作半径为5的圆，则以下四个点在圆上的是（　　）

  A．（3，0）

  B．（0，6）

  C．（2，4）

  D．（3，4）
  组卷：247引用：2难度：0.5

  解析

• 5．关于二次函数y=（x-2）²+6的图象，下列结论不正确的是（　　）

  A．抛物线的开口向上

  B．当x＜1时，y随x的增大而减小

  C．对称轴是直线x=2

  D．抛物线与y轴交于点（0，6）
  组卷：294引用：5难度：0.5

  解析

• 6．从标有2，3，4，5四个数字的卡片中同时抽取两张，记其中一张卡片上的数字为x、另一张卡片上数字为y,这样构成点P的坐标（x,y），那么点P落在双曲线

  y

  =

  6

  x

  上的概率为（　　）

  A． 1 4

  B． 1 12

  C． 1 3

  D． 1 6
  组卷：168引用：3难度：0.5

  解析

• 7．已知点（3，y₁），（-2，y₂），（0，y₃）在抛物线y=x²-2x+c上，则y₁，y₂，y₃的大小关系是（　　）

  A．y3＜y1＜y2

  B．y1＜y3＜y2

  C．y1＜y2＜y3

  D．y2＜y3＜y1
  组卷：239引用：2难度：0.5

  解析

三.解答题（共7小题）

• 22．已知函数

  y

  1

  =

  x

  2

  -

  （

  m

  +

  2

  ）

  x

  +

  2

  m

  +

  3

  ，y₂=nx+k-2n（m,n,k为常数且n≠0）．
  （1）若函数y₁的图象经过点A（2，4），B（-1，3）两个点中的其中一个点，求该函数的表达式．
  （2）若函数y₁，y₂的图象始终经过同一定点M．
  ①求点M的坐标和k的值．
  ②若m+n=-1，当-1＜x＜2时，判断y₁与y₂的大小并说明理由．
  组卷：262引用：1难度：0.3

  解析

• 23．根据以下素材，探索完成任务．

  如何确定拱桥形状？
  问题背景	河面上有一座拱桥，对它的形状，同学们各抒己见．有同学说拱桥的形状是抛物线，也有同学说是圆弧．为确定拱桥的形状，九年级综合实践小组开展了一次探究活动．
  素材1	在正常水位时，小组成员对水面宽度和拱顶离水面的距离进行了测量并绘制了如图．测得水面宽AB为16m,拱顶离水面的距离CD为4m.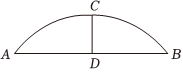
  素材2	大雨过后，水位上涨．小组成员再对水面宽度和拱顶离水面的距离进行了两次测量发现当水面宽为12m时，水位（相对正常水位）上涨1.9m；当水面宽8m时，水位（相对正常水位）上涨3.1m.
  素材3	如何检验探究过程中提出的假设是否符合实际情况呢？ 定义：离差平方和是实际观测值与预测值之间差的平方和，反映了基于假设算得的预测值与实际观测值之间的差异．离差平方和越小，说明预测值与实际观测值之间的误差越小，提出的假设与实际情况更为接近．
  	问题解决
  假设1	小组成员首先假设拱桥形状是抛物线．根据素材1建立如图所示的直角坐标系，求该抛物线的解析式．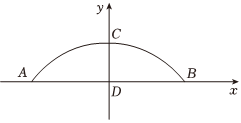
  假设2	小组成员又提出拱桥形状可能是圆弧．请根据素材1求出该圆弧的半径．
  分析判断	于假设1和假设2，请分别计算水面宽12m和8m时水位上涨的预测值，直接填入下表（数据保留两位小数），并结合素材3分别求出两种假设下数据的离差平方和，断拱桥更接近哪一种形状．（参考数据： 21 ≈4.582） 水面宽12m 水面宽8m 水位上涨的实际观测值（m） 1.90 3.10 假设1的预测值（m） 3.00 假设2的预测值（m） 2.00
  组卷：694引用：4难度：0.4

  解析