当前位置：试卷中心 > 试卷详情

2022-2023学年山东省淄博市张店区八年级（下）期末数学试卷（五四学制）

发布：2024/7/7 8:0:9

一、选择题（本题共10小题，每小题4分，共40分．在每小题所给出的四个选项中，只有一个是正确的，请把正确的选项填涂在答题纸的相应位置上）

1．代数式
x
-
3
在实数范围内有意义，则x的取值范围是（　　）
A．x≥3 B．x＞3 C．x≤3 D．x＜3
组卷：757引用：9难度：0.8
解析
2．若
a
b
=
2
3
，则
a
+
b
b
的值为（　　）
A．
2
5
B．
5
2
C．
3
5
D．
5
3
组卷：1007引用：11难度：0.7
解析
3．下列计算中，正确的是（　　）
A．
2
+
2
=
2
2
B．
6
×
3
=
3
2
C．
（
-
2
）
2
=±
2
D．
15
÷
3
=
5
组卷：110引用：4难度：0.7
解析
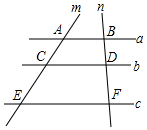4．如图，直线a∥b∥c,直线a,b,c分别交直线m,n于点A，C，E，B，D，F，若AC=2，CE=4，BD=1，则DF=（　　）
A．2 B．3 C．
3
2
D．
7
2
组卷：279引用：1难度：0.7
解析
5．一元二次方程x²-6x-1=0配方后可变形为（　　）
A．（x+3）²=10 B．（x+3）²=8 C．（x-3）²=10 D．（x-3）²=8
组卷：1524引用：27难度：0.8
解析
6．菱形，矩形，正方形都具有的性质是（　　）
A．四条边相等，四个角相等
B．对角线相等
C．对角线互相垂直
D．对角线互相平分
组卷：6243引用：59难度：0.9
解析
7．如图，△ABC与△DEF是位似图形，位似中心为O，OA=2，AD=3，△ABC的面积为4，则△DEF的面积为（　　）
A．6 B．9 C．10 D．25
组卷：197引用：3难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本题共8小题，共计90分，请把解答过程写在答题纸上）

22．【阅读理解】
配方法是中学数学的重要方法，用配方法可求最大（小）值．对于任意正实数a,b,可作如下变形：
∵a+b=
（
a
）
2
+
（
b
）
2
=
（
a
）
2
+
（
b
）
2
-
2
ab
+
2
ab
=
（
a
-
b
）
2
+
2
ab

又∵
（
a
-
b
）
2
≥
0

∴
（
a
-
b
）
2
+
2
ab
≥
0
+
2
ab

即
a
+
b
≥
2
ab
．
根据上述内容，回答问题：2+3
2
2
×
3
；
4
+
1
3

2
4
×
1
3
；6+6
2
6
×
6
．（用“=”“＞”“＜”填空）
【思考验证】
如图1，△ABC中，∠ACB=90°，CD⊥AB于点D，CO为AB边上中线，AD=2a,DB=2b,试根据图形验证
a
+
b
≥
2
ab
成立，并指出等号成立时的条件．
【探索应用】
（1）请利用上述结论解决下面问题，某园林设计师要对园林的一个区域进行设计改造，一面利用墙体将该区域用篱笆围成中间隔有一道篱笆的矩形花圃，如图2所示，为了围成面积为300m²的花圃，所用的篱笆至少为多少米？
（2）如图3，四边形ABCD的对角线AC，BD相交于点O，△AOB，△COD的面积分别是5和16．试问四边形ABCD的面积是否存在最小值？若存在，请直接写出四边形ABCD面积的最小值；若不存在，请说明理由．
组卷：940引用：2难度：0.3
解析
23．已知同一平面内的具有公共顶点C的矩形ABCD和矩形CEFG，且AB=mBC，CG=mCE，连接DG．
（1）当点E是矩形ABCD边AB延长线上的一点时，延长BC交DG于点P．
①如图1，若m=1，猜想线段DP与GP之间的数量关系是
；
②如图2，若m为任意实数，则①中的猜想是否仍然成立？若成立，请给予证明；若不成立，请说明理由；
（2）当点E是平面内任意一点时，取DG的中点Q，如图3所示，连接CQ，BE．若BC=2，CE=3，m=3，请求出CQ的取值范围．
组卷：124引用：1难度：0.3
解析