2022-2023学年四川省乐山市高二（下）期末数学试卷（理科）

一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．计算：（3-4i）（3+4i）=（　　）

  A．-7

  B．7

  C．25

  D．-25
  组卷：25引用：3难度：0.8

  解析

• 2．下列变量间的关系，不是相关关系的是（　　）

  A．一块农田的水稻产量与施肥之间的关系

  B．正方形的面积与边长之间的关系

  C．商品销售收入与其广告费支出之间的关系

  D．人体内的脂肪含量与年龄之间的关系
  组卷：111引用：3难度：0.7

  解析

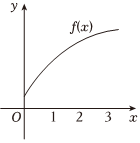• 3．函数y=f（x）的图象如图所示，它的导函数为y=f′（x），下列导数值排序正确的是（　　）

  A．f′（1）＞f′（2）＞f′（3）＞0	B．f′（1）＜f′（2）＜f′（3）＜0
  C．0＜f′（1）＜f′（2）＜f′（3）	D．f′（1）＞f′（2）＞0＞f′（3）
  组卷：193引用：9难度：0.7

  解析

• 4．小李打开计算机时，忘记了开机密码的前两位，他只记得第一位是M，N，R中的一个字母，第二位是1，2，3，4中的一个数字，则小李输入一次密码能成功开机的概率是（　　）

  A． 1 3

  B． 1 4

  C． 1 12

  D． 7 12
  组卷：25引用：2难度：0.7

  解析

• 5．某地为了解中学生的日均睡眠时间（单位：h），随机选择了n位中学生进行调查，根据所得数据画出样本的频率分布直方图，如图所示，且从左到右的第1个，第4个，第2个，第3个小长方形的面积依次构成公差为0.1的等差数列，又第四小组的频数是10，则n等于（　　）

  A．30

  B．40

  C．50

  D．60
  组卷：24引用：3难度：0.7

  解析

• 6．在一次实验中，测得（x,y）的四组数值分别是A（1，3），B（2，3.8），C（3，5.2），D（4，6），则x与y之间的回归直线方程可能是（　　）

  A． ̂ y = - x + 7	B． ̂ y = 1 . 04 x + 1 . 9
  C． ̂ y = 1 . 9 x + 1 . 04	D． ̂ y = 1 . 05 x - 0 . 9
  组卷：20引用：3难度：0.7

  解析

• 7．函数f（x）=x³-3x在区间[-2，0]的最大值和最小值分别为（　　）

  A．2和-2

  B．2和0

  C．1和0

  D．0和-2
  组卷：52引用：3难度：0.7

  解析

三、解答题：共70分，解答应写出文字说明、证明过程或推演步骤.

• 21．如图，在三棱柱ABC-A₁B₁C₁中，侧面BCC₁B₁为正方形，AB=BC=2，AC=2

  3

  ，M，N分别为A₁B₁，AC的中点．
  （1）求证：MN∥平面BCC₁B₁；
  （2）再从条件（1）、条件（2）这两个条件中选择一个作为已知，求二面角A-BM-N的平面角的余弦值．
  条件①：BN⊥平面AA₁C₁C；
  条件②：B₁N=

  5

  ．
  注：如果选择条件①和条件②分别解答，按第一个解答计分．
  组卷：43引用：2难度：0.5

  解析

• 22．已知函数f（x）=e^x-ax和g（x）=ax-lnx有相同的最小值．
  （1）求a；
  （2）若直线y=b与y=f（x）和y=g（x）的图象共有四个不同的交点，试探究：从左到右四个交点横坐标之间的等量关系．
  组卷：18引用：2难度：0.2

  解析