2022-2023学年河北省邯郸市涉县一中高三（上）期中数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合A={x|x²-2x-3＜0}，B={x|x³＜8}，则A∩B=（　　）

  A．（1，2）

  B．（-1，2）

  C．（2，3）

  D．（-3，2）
  组卷：5引用：2难度：0.9

  解析

• 2．在复平面内，复数z₁，z₂对应的点分别是（1，2），（-1，1），则复数z₁•z₂的虚部为（　　）

  A．-i

  B．i

  C．-1

  D．1
  组卷：3引用：2难度：0.8

  解析

• 3．M（2，2）是抛物线y²=2px（p＞0）上一点，F是抛物线的焦点，则|MF|=（　　）

  A． 5 2

  B．3

  C． 7 2

  D．4
  组卷：402引用：5难度：0.8

  解析

• 4．样本中共有5个个体，其中四个值分别为2，2，3，3，第五个值丢失，若该样本的平均数为3，则样本方差为（　　）

  A．1

  B．3

  C． 6 5

  D． 6 25
  组卷：3引用：2难度：0.7

  解析

• 5．过点M（-3，3）作圆C：（x-1）²+y²=25的切线，则切线方程为（　　）

  A．4x+3y+3=0

  B．4x-3y+21=0

  C．x+y=0

  D．x-y+6=0
  组卷：570引用：5难度：0.7

  解析

• 6．窗花是贴在窗纸或窗户玻璃上的剪纸，它是中国古老的传统民间艺术之一，在2022年虎年新春来临之际，人们设计了一种由外围四个大小相等的半圆和中间正方形所构成的剪纸窗花（如图1）．已知正方形ABCD的边长为2，中心为O，四个半圆的圆心均在正方形ABCD各边的中点（如图2），若点P在

  ˆ

  BC

  的中点，则

  （

  PA

  +

  PB

  ）

  •

  PO

  =（　　）
  

  A．2

  B．4

  C．6

  D．8
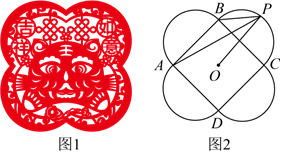  组卷：131引用：8难度：0.7

  解析

• 7．在各项不全为零的等差数列{a_n}中，S_n是其前n项和，且S₉₉=0，S_k=S₉₀（k≠90），则正整数k的值为（　　）

  A．11

  B．10

  C．9

  D．8
  组卷：9引用：2难度：0.7

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．若在数列的每相邻两项之间插入此两项的和，形成新的数列，再把所得数列按照同样的方法不断构造出新的数列．现对数列1，2进行构造，第一次得到数列1，3，2；第二次得到数列1，4，3，5，2；依次构造，第n（n∈N^*）次得到的数列的所有项之和记为a_n．
  （1）求a_n+1与a_n满足的关系式；
  （2）求数列{a_n}的通项公式a_n；
  （3）证明：

  1

  a

  1

  +

  1

  a

  2

  +

  1

  a

  3

  +

  ⋯

  +

  1

  a

  n

  ＜

  1

  3

  ．
  组卷：47引用：3难度：0.4

  解析

• 22．已知a＞0，函数f（x）=ae^x-ln（ax+a）．
  （1）当a=1时，求f（x）的单调区间；
  （2）证明：f（x）≥1．
  组卷：68引用：3难度：0.5

  解析