2022-2023学年湖北省问津联合体高二(上)期中数学试卷
发布:2024/8/22 1:0:1
一、选择题(共8小题,每小题5分,满分40分)
-
1.直线x+
y-1=0的倾斜角为( )3组卷:480引用:25难度:0.9 -
2.已知椭圆
+y2=1,则该椭圆的焦距为( )x24组卷:236引用:2难度:0.8 -
3.已知直线l1:(k-3)x+(4-k)y+1=0与l2:2(k-3)x-2y+3=0平行,则k的值是( )
组卷:125引用:4难度:0.9 -
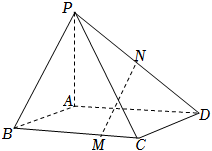 4.已知四棱锥P-ABCD,底面ABCD为平行四边形,M,N分别为棱BC,PD上的点,,PN=ND,设CMCB=13,AB=a,AD=b,则向量AP=c用MN为基底表示为( ){a,b,c}组卷:828引用:20难度:0.7
4.已知四棱锥P-ABCD,底面ABCD为平行四边形,M,N分别为棱BC,PD上的点,,PN=ND,设CMCB=13,AB=a,AD=b,则向量AP=c用MN为基底表示为( ){a,b,c}组卷:828引用:20难度:0.7 -
 5.如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,,AC=1,则异面直线AC1与CB1所成角的余弦值为( )BC=AA1=3组卷:71引用:5难度:0.6
5.如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,,AC=1,则异面直线AC1与CB1所成角的余弦值为( )BC=AA1=3组卷:71引用:5难度:0.6 -
6.若直线y=k(x-4)+2与曲线
恰有两个交点,则实数k的取值范围是( )x=4-y2组卷:250引用:8难度:0.6 -
7.已知点F1(-2,0),圆F2:(x-2)2+y2=36,点M是圆上一动点,线段MF1的垂直平分线与MF2交于点N.则点N的轨迹方程为( )
组卷:19引用:1难度:0.7
四、解答题(共6小题,满分70分)
-
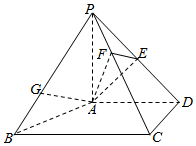 21.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且=PFPC.13
21.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且=PFPC.13
(Ⅰ)求证:CD⊥平面PAD;
(Ⅱ)求二面角F-AE-P的余弦值;
(Ⅲ)设点G在PB上,且=PGPB.判断直线AG是否在平面AEF内,说明理由.23组卷:5585引用:21难度:0.8 -
22.已知椭圆C:
x2a2=1(a>b>0)的长轴长是短轴长的+y2b2倍,且经过点(2).2,1
(1)求C的标准方程;
(2)已知C的右顶点为A,过C右焦点的直线l与C交于不同的两点M,N,求△AMN面积的最大值.组卷:43引用:6难度:0.3


