2022-2023学年江苏省连云港市灌云县西片九年级(下)月考数学试卷(5月份)
发布:2024/5/14 8:0:9
一.选择题(共8小题)
-
1.在实数
,3,0,-1中,最小的数是( )13组卷:120引用:7难度:0.9 -
2.下列运算正确的是( )
组卷:156引用:7难度:0.7 -
 3.下列几何体中,主视图为如图的是( )组卷:20引用:5难度:0.6
3.下列几何体中,主视图为如图的是( )组卷:20引用:5难度:0.6 -
4.在战“疫”诗歌创作大赛中,有7名同学进入了决赛,他们的最终成绩均不同.小弘同学想知道自己能否进入前3名,除要了解自己的成绩外,还要了解这7名同学成绩的( )
组卷:218引用:14难度:0.6 -
5.在平面直角坐标系中,以点(-3,4)为圆心,3为半径的圆( )
组卷:1783引用:9难度:0.5 -
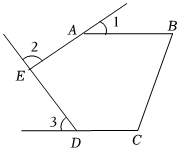 6.如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3是外角,则∠1+∠2+∠3等于( )组卷:1083引用:11难度:0.7
6.如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3是外角,则∠1+∠2+∠3等于( )组卷:1083引用:11难度:0.7 -
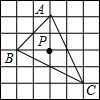 7.△ABC在正方形网格中的位置如图所示,点A,B,C,P均在格点上,则点P是△ABC的( )组卷:585引用:6难度:0.7
7.△ABC在正方形网格中的位置如图所示,点A,B,C,P均在格点上,则点P是△ABC的( )组卷:585引用:6难度:0.7 -
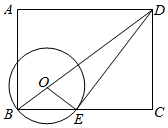 8.如图,在矩形ABCD中,AB=6,AD=8,点O在对角线BD上,以OB为半径作⊙O交BC于点E,连接DE,若DE是⊙O的切线,此时⊙O的半径为( )组卷:2356引用:11难度:0.3
8.如图,在矩形ABCD中,AB=6,AD=8,点O在对角线BD上,以OB为半径作⊙O交BC于点E,连接DE,若DE是⊙O的切线,此时⊙O的半径为( )组卷:2356引用:11难度:0.3
二.填空题(共8小题)
-
9.计算
的结果是 .(-2023)2组卷:319引用:6难度:0.8
三.解答题(共11小题)
-
26.(1)[问题提出]:如图1,AB为⊙O的直径,点C为⊙O上一点,连接AC、BC,若AB=6,则△ABC面积的最大值为 .
(2)[问题探究]:如图2,在四边形ABCD中,∠B=∠D=90°,∠C=60°,AB=AD,点E、F分别在边BC、CD上.且∠EAF=60°,若BE=3,EF=10,求DF的长;
(3)[问题解决]:为进一步落实国家“双减”政策,丰富学生的校园生活,某校计划为同学们开设实践探究课.按规划要求,需设计一个正方形的研学基地,如图3.点E、F分别在正方形ABCD的边BC、CD上,将△AEF区域修建为种植采摘区,基地内其余部分为研学探究区,BE+DF的长为40m,∠EAF=45°.为了让更多的学生能够同时进行种植,要求种植采摘区(△AEF)的面积尽可能大,则种植采摘区的面积的最大值为 m2,此时正方形ABCD的边长为 m.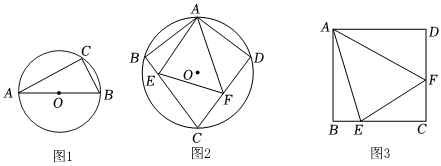 组卷:207引用:4难度:0.1
组卷:207引用:4难度:0.1 -
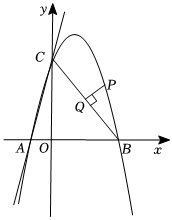 27.如图,在平面直角坐标系中,直线y=4x+4与x轴交于A点,与y轴交于C点,抛物线)经过A,C两点,与x轴相交于另一点B,连接BC.点P是线段BC上方抛物线上的一个动点,过点P作PQ⊥BC交线段BC于点Q.y=ax2+83x+c(a≠0)
27.如图,在平面直角坐标系中,直线y=4x+4与x轴交于A点,与y轴交于C点,抛物线)经过A,C两点,与x轴相交于另一点B,连接BC.点P是线段BC上方抛物线上的一个动点,过点P作PQ⊥BC交线段BC于点Q.y=ax2+83x+c(a≠0)
(1)求抛物线的解析式;
(2)点D为抛物线对称轴上的一个动点,则|DC-DB|的最大值是 ;
(3)求PQ的最大值,并写出此时点P的坐标;
(4)在x轴上找一点M,抛物线上找一点N,使以点B,C,M,N为顶点的四边形是平行四边形,请直接写出点M的坐标.组卷:361引用:4难度:0.3


