2022-2023学年辽宁省朝阳市凌源市高二（上）月考数学试卷（10月份）

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知直线l经过点（1，-2），（3，0），则直线l的倾斜角为（　　）

  A． π 4

  B． π 3

  C． 2 π 3

  D． 3 π 4
  组卷：129引用：8难度：0.8

  解析

• 2．若复数z=m²-25+（m-5）i是纯虚数，则m=（　　）

  A．-5

  B．5

  C．25

  D．±5
  组卷：121引用：2难度：0.8

  解析

• 3．以点（-3，2）为圆心，且与直线3x-y+1=0相切的圆的方程是（　　）

  A．（x-3）2+（y+2）2=10	B．（x+3）2+（y-2）2=1
  C．（x+3）2+（y-2）2=10	D．（x-3）2+（y+2）2=1
  组卷：239引用：7难度：0.6

  解析

• 4．设α，β为两个不同平面，直线m⊂α，则“α∥β”是“m∥β”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：179引用：22难度：0.9

  解析

• 5．若幂函数f（x）=（m²+m-5）x^m-1在（0，+∞）上单调递减，则m=（　　）

  A．-3或2

  B．2

  C．-3

  D．-2
  组卷：410引用：4难度：0.7

  解析

• 6．若圆锥的轴截面为等边三角形，且面积为

  4

  3

  ，则圆锥的体积为（　　）

  A． 4 3 π

  B． 4 3 π 3

  C． 8 3 π 3

  D． 8 3 π
  组卷：71引用：3难度：0.7

  解析

• 7．已知函数f（x）=2sin（ωx+φ）（ω＞0，0

  ＜

  φ

  ＜

  π

  2

  ）的图象的相邻两个最高点的距离为

  π

  2

  ，

  f

  （

  0

  ）

  =

  2

  ，则f（x）=（　　）

  A． 2 sin （ 2 x + π 4 ）	B． 2 sin （ 2 x + π 4 ）
  C． 2 sin （ 4 x + π 4 ）	D． 2 sin （ 4 x + π 4 ）
  组卷：214引用：4难度：0.7

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

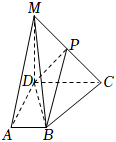• 21．已知四棱锥M-ABCD的底面为直角梯形，AB∥CD，∠ADC=90°，MD⊥底面ABCD，且MD=DC=AD=2AB=2，P是MC的中点．
  （1）证明：BP∥平面MAD；
  （2）求直线MB与平面DBP所成角的正弦值．
  组卷：201引用：11难度：0.7

  解析

• 22．已知⊙C的方程是x²+y²-6x-8y+21=0，直线l经过点P（1，0）．
  （1）若直线l与⊙C相切，求直线l的方程；
  （2）若直线l与⊙C相交于A，B两点，与直线l₁：x+2y+2=0交于点M，求证：

  PA

  •

  PM

  +

  PB

  •

  PM

  为定值．
  组卷：37引用：4难度：0.4

  解析