2023-2024学年北京八十中高二（上）段考数学试卷（10月份）

一、选择题（本题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项符合题目要求）

• 1．在空间直角坐标系Oxyz中，点A（2，3，4）关于原点的对称点坐标为（　　）

  A．（2，3，-4）

  B．（-2，3，-4）

  C．（-2，-3，-4）

  D．（2，-3，-4）
  组卷：30引用：3难度：0.8

  解析

• 2．设A是空间一定点，

  n

  为空间内任一非零向量，满足条件

  AM

  •

  n

  =0的点M构成的图形是（　　）

  A．圆

  B．线段

  C．直线

  D．平面
  组卷：100引用：8难度：0.6

  解析

• 3．已知空间向量

  a

  +

  b

  +

  c

  =

  0

  ，|

  a

  |=2，|

  b

  |=3，|

  c

  |=4，则cos＜

  a

  ，

  b

  ＞=（　　）

  A． 1 2

  B． 1 3

  C．- 1 2

  D． 1 4
  组卷：559引用：9难度：0.7

  解析

• 4．如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，已知

  PA

  =

  a

  ，

  PB

  =

  b

  ，

  PC

  =

  c

  ，

  PE

  =

  1

  2

  PD

  ，则

  BE

  =（　　）

  A． 1 2 a - 3 2 b + 1 2 c	B． 1 2 a + 1 2 b + 1 2 c
  C．- 1 2 a - 3 2 b + 1 2 c	D．- 1 2 a - 1 2 b + 3 2 c
  组卷：112引用：12难度：0.7

  解析

• 5．若直线l的方向向量为

  b

  ，平面α的法向量为

  n

  ，则可能使l∥α的是（　　）

  A． b =（1，0，0）， n =（-2，0，0）

  B． b =（1，3，5）， n =（1，0，1）

  C． b =（0，2，1）， n =（-1，0，-1）

  D． b =（1，-1，3）， n =（0，3，1）
  组卷：190引用：18难度：0.9

  解析

• 6．已知向量

  a

  =（1，x,-2），

  b

  =（0，1，2），

  c

  =（1，0，0），若

  a

  ，

  b

  ，

  c

  共面，则x等于（　　）

  A．-1

  B．1

  C．1或-1

  D．1或0
  组卷：1317引用：9难度：0.9

  解析

三、解答题（本题共4小题，共40分．解答应写出文字说明、证明过程或演算步骤．）

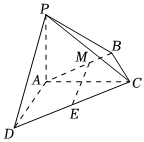• 18．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BCA=60°，AP=AC=AD=2，E为CD的中点，M在AB上，且

  AM

  =2

  MB

  ．
  （Ⅰ）求证：EM∥平面PAD；
  （Ⅱ）求平面PAD与平面PBC所成锐二面角的余弦值；
  （Ⅲ）点F是线段PD上异于两端点的任意一点，若满足异面直线EF与AC所成角45°，求AF的长．
  组卷：954引用：10难度：0.3

  解析

• 19．如图，在四棱柱ABCD-A₁B₁C₁D₁中，A₁A⊥底面ABCD，∠BAD=90°．AD∥BC．且A₁A=AB=AD=2BC=2，点E在棱AB上，平面A₁EC与棱C₁D₁相交于点F．
  
  （Ⅰ）证明：A₁F∥平面B₁CE；
  （Ⅱ）棱AB上是否存在点E，使二面角A₁-EC-D的余弦值为

  1

  3

  ？若存在，求出

  AE

  AB

  的值；若不存在，说明理由．
  （Ⅲ）求三棱锥B₁-A₁EF的体积的最大值．
  组卷：181引用：2难度：0.5

  解析