2022-2023学年浙江省金华市东阳市江北初级中学等四校联考九年级（下）月考数学试卷（5月份）
发布：2024/7/11 8:0:9
一、选择题。（本题有10小题，每小题3分，共30分）
-
1．四个实数1，
，2，-2中，比0小的数是（ ）15组卷：4引用：1难度：0.8 -
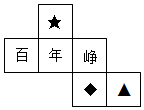2．一个正方体的表面分别标有百、年、峥、嵘、岁、月，下面是该正方体的一个展开图，已知“嵘”的对面为“岁”，则（ ）组卷：600引用：9难度：0.7 -
3．下列表格列举了2022卡塔尔世界杯优秀球员射门数据，观察表格中的数据，这组数据的中位数和众数分别是（ ）
球员 梅西 姆巴佩 佩里西奇 吉鲁 马丁内斯 奥尔莫 得分 32 31 16 16 14 12 组卷：89引用：2难度：0.6 -
4．已知∠a=34°30'，则它的补角为（ ）
组卷：46引用：1难度：0.9 -
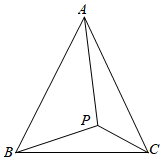5．如图，在△ABC中，AB=AC，点P为△ABC内一点，连接PA、PB、PC，∠APB≠∠APC，求证：PB≠PC，用反证法证明时，第一步应假设（ ）组卷：427引用：5难度：0.7 -
6．要判断一个四边形是否为菱形，可行的测量方案是（ ）
组卷：71引用：1难度：0.5 -
7．已知9m=3，27n=4，则32m+3n=（ ）
组卷：5965引用：36难度：0.8 -
8．如图，在平面直角坐标系中，菱形ABOC的顶点O在坐标原点，边BO在x轴的负半轴上，∠BOC=60°，顶点C的坐标为，反比例函数（m,3）的图象与菱形对角线AO交于D点，连接BD，当DB⊥x轴时，k的值是（ ）y=kx
组卷：115引用：1难度：0.5
三、解答题。（本题有8小题，共66分，各小题都必须写出解答过程）
-
23．【阅读理解】：
关于x的函数y=mx-2m-3（m为常数，且m≠0），经过某个定点，请求出定点的坐标．
方法一：先将等式化为（x-2）m=y+3的形式，再根据0m=0时有m无数多个解，求得定点的坐标为（2，-3）；
方法二：当m=1时，y=x-5；当m=2时，y=2x-7；
解方程组解得y=x-5y=2x-7，x=2y=-3
∴求得定点的坐标为（2，-3）
【模仿练习】
关于x的二次函数 y=mx2+（2m+1）x+1（ 为常数，且m≠0），是否经过定点，如果是，请选择一种方法求出定点的坐标；如果不是，请说明理由．
【尝试应用】某“数学兴趣小组”根据学习函数的经验，对函数y=-（x-1）（|x|-3）的图象和性质进行了探究，探究过程如下，请补充完整：
（1）计算x与y的几组对应值，其中m=；
列表如下：x … -4 -3 -2 -1 0 1 2 3 4 … y … 5 0 -3 m -3 0 1 0 -3 …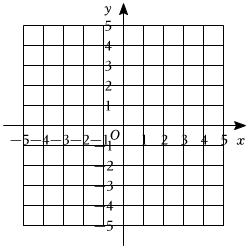 
（2）如图，在直角坐标系中用描点法画出了函数y=-（x-1）（|x|-3）这个图象；
（3）若直线y=tx-2t+2与函数y=-（x-1）（|x|-3）（2＜x≤4）的图象只有一个交点，请结合函数图象，求出t的取值范围．组卷：255引用：3难度：0.3 -
24．如图1，已知在矩形ABCD中，点E在边AB上，△BEC与△FEC关于直线EC对称，点B的对称点F在边AD上，
（1）求证：△AEF∽△DFC；
（2）如图2，G为CD的中点，连结BG分别与CE，CF相交于M，N两点．若BE=BM，MG=2，求CD的长度；
（3）在（2）的条件下求出BN的长度和cos∠AEF的值；
（4）在（2）的条件下求出EF的长度．
组卷：81引用：1难度：0.1
