2021-2022学年四川省眉山市高二（上）期末数学试卷（文科）

一、选择题（共12小题，每小题5分，满分60分）

• 1．抛物线x²=

  1

  2

  y

  的焦点到准线的距离是（　　）

  A．2

  B．1

  C． 1 2

  D． 1 4
  组卷：68引用：15难度：0.9

  解析

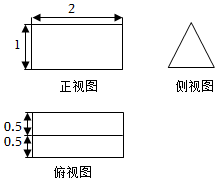• 2．某空间几何体的三视图如图所示，则其体积为（　　）

  A．2

  B． 2 3

  C．1

  D． 1 3
  组卷：57引用：2难度：0.7

  解析

• 3．圆x²+y²=4与圆（x-3）²+（y-4）²=49的位置关系为（　　）

  A．内切

  B．相交

  C．外切

  D．相离
  组卷：159引用：6难度：0.8

  解析

• 4．l,m,n是三条不同的直线，α，β，γ是三个不同的平面，下列命题中正确的是（　　）

  A．若α⊥β，β⊥γ，α∩γ=l,则l⊥β

  B．若m⊥n,n⊥l,则m∥l

  C．若α∥β，m⊂α，n⊂β，则m∥n

  D．若l∥α，α⊥β，则l⊥β
  组卷：467引用：5难度：0.4

  解析

• 5．若m,n是两条不重合的直线，α是一个平面，且n⊥α，则“m⊥n”是“m∥α”的（　　）

  A．充分必要条件	B．充分不必要条件
  C．必要不充分条件	D．既不充分也不必要条件
  组卷：30引用：2难度：0.7

  解析

• 6．若圆x²+y²+2x-6y+6=0有且仅有三个点到直线x+ay+1=0的距离为1，则实数a的值为（　　）

  A．±1

  B． ± 2 4

  C． ± 2

  D． ± 3 2
  组卷：291引用：13难度：0.7

  解析

• 7．已知双曲线C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的右焦点到渐近线的距离等于实轴长，则此双曲线的离心率为（　　）

  A． 5

  B．5

  C． 2

  D．2
  组卷：142引用：30难度：0.7

  解析

三.解答题：本大题共6小题，共70分，解答应写出文字说明、证明过程或推演步骤.

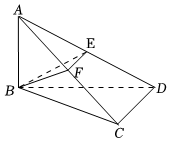• 21．如图，已知AB⊥平面BCD，平面ABC⊥平面ACD，E，F分别是AD，AC的中点．
  （1）求证：BC⊥CD；
  （2）若BD=2AB=4，直线BD与平面ABC所成角为30°，求三棱锥A-BEF的体积．
  组卷：142引用：1难度：0.6

  解析

• 22．设抛物线y²=2px（p＞0）上位于第一象限的点M与焦点F的距离为

  5

  2

  ，点M到x轴的距离为2p,直线l与抛物线相交于A，B两点，且MA⊥MB．
  （1）求抛物线的方程和点M的坐标；
  （2）求证：直线l恒过定点（4，-2）．
  组卷：37引用：1难度：0.6

  解析