2022-2023学年湖北省咸宁市高一(下)期末数学试卷
发布:2024/6/23 8:0:10
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知集合M={z∈C||z|=2},则( )
组卷:35引用:3难度:0.8 -
2.已知x>3,y=x+
,则y的最小值为( )1x-3组卷:840引用:8难度:0.9 -
3.若一个圆锥的侧面展开图是半径为2,圆心角为180°的扇形,则该圆锥的高为( )
组卷:103引用:3难度:0.8 -
4.设α,β为两个不同的平面,则α∥β的一个充分条件可以是( )
组卷:448引用:10难度:0.7 -
5.定义在R上的函数f(x)满足f(x+2)+f(x)=3,且f(1)=0,则f(2023)=( )
组卷:434引用:4难度:0.7 -
6.若存在实数m,使得
,则实数a的取值范围是( )loga4<m<2a-1组卷:20引用:3难度:0.8 -
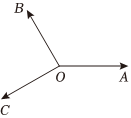 7.如图,已知平面向量满足OA、OB、OC,则( )|OA|=|OB|=|OC|,〈OA,OB〉=120°,OB⊥OC组卷:40引用:3难度:0.8
7.如图,已知平面向量满足OA、OB、OC,则( )|OA|=|OB|=|OC|,〈OA,OB〉=120°,OB⊥OC组卷:40引用:3难度:0.8
四、解答题:本题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.
-
21.在△ABC中,A,B,C所对的边分别为a,b,c,已知sinA=tanB.
(1)若,求C的值;a=2c
(2)若A为锐角,求的取值范围.b+ca组卷:61引用:2难度:0.5 -
22.已知f(x)=ax-a-x,g(x)=ax+a-x,其中a>0,a≠1.
(1)若g(2x+1)≤g(x+2),求x的取值范围.
(2)设,若F(x)=f(x)g(x),恒有∀x1,x2∈[12,1],求a的取值范围.F(2x1)F(x1)≥1817×g(4x2)g(2x2)组卷:42引用:3难度:0.4


