2022-2023学年湖北省随州市曾都一中高二（上）月考数学试卷（11月份）

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．抛物线y²=-7x的准线方程为（　　）

  A． x = 7 8

  B． y = 7 8

  C． x = 7 4

  D． y = 7 4
  组卷：21引用：2难度：0.7

  解析

• 2．已知空间向量

  a

  =

  （

  6

  ，-

  3

  ，

  1

  ）

  与

  b

  =

  （

  3

  ，

  x

  ,

  y

  ）

  共线，则x-y=（　　）

  A．-1

  B．2

  C．-2

  D．1
  组卷：69引用：2难度：0.8

  解析

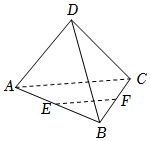• 3．如图所示，在三棱锥D-ABC中，E，F分别是AB，BC的中点，则

  DA

  +

  1

  2

  AB

  +

  1

  2

  AC

  等于（　　）

  A． DE

  B． ED

  C． DC

  D． DF
  组卷：179引用：2难度：0.7

  解析

• 4．若抛物线x²=2my的焦点与椭圆

  x

  2

  3

  +

  y

  2

  4

  =

  1

  的上焦点重合，则m的值为（　　）

  A．2

  B．4

  C．-2

  D．-4
  组卷：84引用：2难度：0.7

  解析

• 5．已知x,y是实数，且x²+y²-4x+1=0，则

  y

  +

  2

  x

  +

  1

  的最大值是（　　）

  A． 6 - 30 6

  B． 11 6

  C． 33 6

  D． 6 + 30 6
  组卷：96引用：2难度：0.6

  解析

• 6．已知椭圆C₁：

  x

  2

  49

  +

  y

  2

  7

  =1与双曲线C₂：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1有共同的焦点F₁，F₂，且曲线C₁，C₂在第一象限内的公共点记为P，若∠F₁PF₂=

  2

  π

  3

  ，则双曲线C₂的离心率为（　　）

  A． 2

  B． 3

  C． 3 2 4

  D． 3 3 4
  组卷：151引用：4难度：0.6

  解析

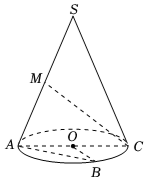• 7．如图，某圆锥SO的轴截面SAC是等边三角形，点B是底面圆周上的一点，且∠BOC
  =60°，点M是SA的中点，则异面直线AB与CM所成角的余弦值是（　　）

  A． 1 3

  B． 7 4

  C． 3 4

  D． 3 2
  组卷：333引用：12难度：0.8

  解析

四、解答题：本题共6小题，共70分．解答应写出必要的文字说明、证明过程及演算步骤．

• 21．已知圆C：（x+1）²+y²=16，定点F（1，0），Q为圆上的一动点，点P在半径CQ上，且

  QF

  •（

  PQ

  +

  PF

  ）=0，设点P的轨迹为曲线E．
  （1）求曲线E的方程；
  （2）过点H（0，2）的直线交曲线E于A，B两点，过点H与AB垂直的直线与x轴交于点N，当

  |

  AB

  |

  |

  HN

  |

  取最大值时，求直线AB的方程．
  组卷：120引用：4难度：0.6

  解析

• 22．已知双曲线C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）过点P（3

  2

  ，4），且C的渐近线方程为y=±

  4

  3

  x.
  （1）求C的方程．
  （2）A，B为C的实轴端点，Q为C上异于A，B的任意一点，QA，QB与y轴分别交于M，N两点，证明：以MN为直径的圆过两个定点．
  组卷：134引用：4难度：0.4

  解析