2022-2023学年湖北省武汉市武昌实验中学高二（上）月考数学试卷（10月份）

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．设a∈R，则“a=-1”是“直线ax+y-1=0与直线x+ay+5=0平行”的（　　）

  A．充分而不必要条件	B．必要而不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：329引用：23难度：0.9

  解析

• 2．在正方体ABCD-A₁B₁C₁D₁中，P，Q分别为B₁C₁，BC的中点，则异面直线AQ与BP所成角的余弦值是（　　）

  A． 1 5

  B． 2 5

  C． 1 10

  D． 5 5
  组卷：86引用：3难度：0.7

  解析

• 3．已知点（m,n）在过（-2，0）点且与直线2x-y=0垂直的直线上，则圆C：

  （

  x

  -

  3

  5

  ）

  2

  +

  （

  y

  +

  1

  ）

  2

  =

  4

  上的点到点M（m,n）的轨迹的距离的最小值为（　　）

  A．1

  B．2

  C．5

  D． 3 5
  组卷：59引用：4难度：0.6

  解析

• 4．如果圆（x-a）²+（y-a）²=8上总存在两个点到原点的距离为

  2

  ，则实数a的取值范围是（　　）

  A．（-3，3）	B．（-1，1）
  C．（-3，1）	D．（-3，-1）∪（1，3）
  组卷：220引用：2难度：0.7

  解析

• 5．阅读材料：空间直角坐标系O-xyz中，过点P（x₀，y₀，z₀）且一个法向量为

  n

  =

  （

  a

  ,

  b

  ,

  c

  ）

  的平面α的方程为a（x-x₀）+b（y-y₀）+c（z-z₀）=0，阅读上面材料，解决下面问题：已知平面α的方程为3x-5y+z-7=0，直线l是两平面x-3y+7=0与4y+2z+1=0的交线，则直线l与平面α所成角的正弦值为（　　）

  A． 10 35

  B． 7 5

  C． 7 15

  D． 14 55
  组卷：293引用：22难度：0.7

  解析

• 6．我国魏晋时期的数学家刘徽创立了割圆术，也就是用圆内接正多边形去逐步逼近圆，即圆内接正多边形边数无限增加时，其周长就越逼近圆周长，这种用极限思想解决数学问题的方法是数学史上的一项重大成就．现作出圆x²+y²=2的一个内接正八边形，使该正八边形的其中4个顶点在坐标轴上，则下列4条直线中不是该正八边形的一条边所在直线的为（　　）

  A．x+（ 2 -1）y- 2 =0	B．（1- 2 ）x-y+ 2 =0
  C．x-（ 2 +1）y+ 2 =0	D．（ 2 -1）x-y+ 2 =0
  组卷：142引用：9难度：0.5

  解析

• 7．过直线x+y+2=0上一点P，作圆（x-3）²+（y+1）²=16的两条切线，切点分别为A（x₁，y₁），B（x₂，y₂），若y₂²-y₁²=（x₁-x₂）（x₁+x₂-2），则|PA|=（　　）

  A．8

  B． 4 5

  C． 4 13

  D．10
  组卷：143引用：2难度：0.8

  解析

四、解答题：本大题共6个大题，共70分，解答应写出文字说明、证明过程或演算步骤．

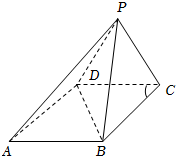• 21．如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠DCB=60°，AB⊥PB．
  （1）证明：△PDC为等腰三角形；
  （2）若平面PDC⊥平面ABCD，AB=2，求二面角A-PB-C的余弦值的取值范围．
  组卷：99引用：6难度：0.6

  解析

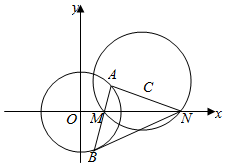• 22．如图，圆C：x²-（1+a）x+y²-ay+a=0．
  （1）若圆C与y轴相切，求圆C的方程；
  （2）当a=4时，圆C与x轴相交于两点M，N（点M在点N的左侧）．问：是否存在圆O：x²+y²=r²，使得过点M的任一条直线与该圆的交点A，B，都有∠ANM=∠BNM？若存在，求出圆方程，若不存在，请说明理由．
  组卷：890引用：7难度：0.3

  解析