2022-2023学年山西省吕梁市交口县七年级（下）期末数学试卷

一、选择题（本大题共10个小题，每小题3分，共30分）

• 1．杭州第19届亚运会将于2023年9月23日至10月8日举行，亚运会将在主办城市杭州和宁波、温州、金华、绍兴、湖州等五个协办城市举办．以下通过平移杭州亚运会会徽得到的图形是（　　）

  A．

  B．

  C．

  D．
  组卷：126引用：3难度：0.5

  解析

• 2．下列实数中，无理数是（　　）

  A．2

  B．- 1 2

  C．3.14

  D． 3
  组卷：440引用：8难度：0.9

  解析

• 3．平面直角坐标系中，点A（-1，-3）在第（　　）象限．

  A．一

  B．二

  C．三

  D．四
  组卷：199引用：7难度：0.9

  解析

• 4．下列方程中，属于二元一次方程的是（　　）

  A．2x+3=x-5

  B．xy+y=2

  C．3x-1=2-5y

  D．2x+ 3 y =7
  组卷：317引用：6难度：0.9

  解析

• 5．下列计算正确的是（　　）

  A． 4 =±2

  B． 36 =6

  C． （ - 6 ） 2 =-6

  D．- 3 - 8 =-2
  组卷：1332引用：9难度：0.8

  解析

• 6．要调查下列问题，适合采用全面调查的是（　　）

  A．中央电视台某一期《最强大脑》的收视率

  B．交口县某社区居民5月份人均网上购物的次数

  C．天舟六号的零部件质量

  D．比亚迪新能源汽车护卫舰07的最大续航里程
  组卷：50引用：3难度：0.5

  解析

• 7．解方程组

  4 x - 3 y = 2 ①

  4 x + y = 10 ②

  时，由②-①得（　　）

  A．4y=8

  B．2y=8

  C．-2y=8

  D．-4y=8
  组卷：874引用：5难度：0.9

  解析

三、解答题（本大题共8个小题，共70分）

• 22．在2022年卡塔尔世界杯期间，某商店分两次购入某款纪念册和吉祥物两种商品，若两次进价相同，第一次购入25件纪念册和20件吉祥物共花费5250元，第二次购入20件纪念册和25件吉祥物共花费6000元．
  （1）分别求出每件纪念册和每件吉祥物的进价．
  （2）为满足市场需求，商店准备第三次购入纪念册和吉祥物共500件．若进价不变，纪念册与吉祥物的单件售价分别为65元、220元的情况下，要使得商店获得利润不低于9165元，最多应购入纪念册多少件？
  组卷：28引用：2难度：0.5

  解析

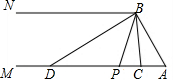• 23．问题情境
  在综合实践课上，老师组织七年级（2）班的同学开展了探究两角之间数量关系的数学活动，如图，已知射线AM∥BN，连接AB，点P是射线AM上的一个动点（与点A不重合），BC，BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D．
  探索发现
  “快乐小组”经过探索后发现：
  （1）当∠A=60°时，求证：∠CBD=∠A．
  （2）不断改变∠A的度数，∠CBD与∠A却始终存在某种数量关系，
  当∠A=40°，则∠CBD=

  度，
  当∠A=x°时，则∠CBD=

  度，（用含x的代数式表示）
  操作探究
  （3）“智慧小组”利用量角器量出∠APB和∠ADB的度数后，探究二者之间的数量关系．他们惊奇地发现，当点P在射线AM上运动时，无论点P在AM上的什么位置，∠APB与∠ADB之间的数量关系都保持不变，请写出它们的关系，并说明理由．
  组卷：477引用：6难度：0.5

  解析