2023-2024学年山东省青岛市市南区九年级(上)月考数学试卷(10月份)
发布:2024/9/1 5:0:10
一、选择题(共10题,每题3分)
-
1.下列说法中,错误的是( )
组卷:1876引用:18难度:0.6 -
2.要检验一个四边形的桌面是否为矩形,可行的测量方案是( )
组卷:2720引用:23难度:0.5 -
3.一个不透明的袋子中装有仅颜色不同的2个红球和2个白球,两个人依次从袋子中随机摸出一个小球不放回,则第一个人摸到红球且第二个人摸到白球的概率是( )
组卷:139引用:3难度:0.7 -
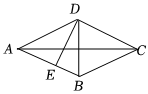 4.如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )组卷:778引用:5难度:0.6
4.如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )组卷:778引用:5难度:0.6 -
5.用配方法解一元二次方程3x2-6x-5=0时,下列变形正确的是( )
组卷:720引用:4难度:0.7 -
 6.如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段,则线段AB的长是( )AC=152组卷:1757引用:21难度:0.5
6.如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段,则线段AB的长是( )AC=152组卷:1757引用:21难度:0.5 -
7.如图①所示,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个面积为20cm2的长方形,将不规则图案围起来,然后在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或长方形区域外不计试验结果),他将若干次有效试验的结果绘制成了如图②所示的折线统计图,由此他估计不规则图案的面积大约为( )
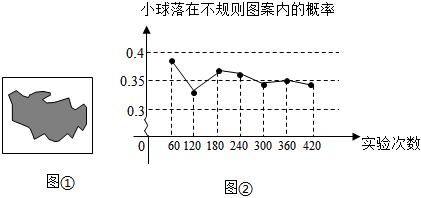 组卷:762引用:13难度:0.5
组卷:762引用:13难度:0.5 -
8.三角形两边长分别为7和4,第三边是方程x2-11x+18=0的解,则这个三角形的周长是( )
组卷:799引用:7难度:0.7
三、解答题。(共8题,72分)
-
23.阅读材料:
材料1:关于x的一元二次方程ax2+bx+c=0(a≠0)的两个实数根x1,x2和系数a、b、c,有如下关系:x1+x2=-,x1x2=ba.ca
材料2:已知一元二次方程x2-x-1=0的两个实数根分别为m,n,求m2n+mn2的值.
解:∵m,n是一元二次方程x2-x-1=0的两个实数根.
∴m+n=1,mn=-1.
则m2n+mn2=mn(m+n)=-1×1=-1.
根据上述材料,结合你所学的知识,完成下列问题.
(1)应用:一元二次方程2x2+3x-1=0的两个实数根为x1,x2,则x1+x2=,x1x2=.
(2)类比:已知一元二次方程2x2+3x-1=0的两个实数根为m、n,求m2+n2的值;
(3)提升:已知实数s,t满足2s2+3s-1=0,2t2+3t-1=0,且s≠t.
求:①4s2+7s+t;
②-1s的值.1t组卷:632引用:3难度:0.5 -
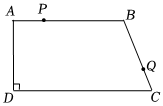 24.如图,在四边形ABCD中,AB∥CD,∠ADC=90°,AD=12cm,AB=18cm,CD=23cm,动点P从点A出发,以1cm/s的速度向终点B运动,同时动点Q从点B出发,以2cm/s的速度沿折线B-C-D向终点D运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t秒.
24.如图,在四边形ABCD中,AB∥CD,∠ADC=90°,AD=12cm,AB=18cm,CD=23cm,动点P从点A出发,以1cm/s的速度向终点B运动,同时动点Q从点B出发,以2cm/s的速度沿折线B-C-D向终点D运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t秒.
(1)用含t的式子表示PB.
(2)当t为何值时,直线PQ把四边形ABCD分成两个部分,且其中的一部分是平行四边形?
(3)只改变点Q的运动速度,使运动过程中某一时刻四边形PBCQ为菱形,则点Q的运动速度应为多少?组卷:1360引用:5难度:0.3


