2020-2021学年广东省东莞市光正实验学校九年级（上）期中数学试卷

一、选择题（本题共有10小题，每小题3分，共30分）

• 1．关于x的一元二次方程（m-1）x²+3x+m²-1=0的一根为0，则m的值是（　　）

  A．-1

  B．-2

  C．±1

  D．±2
  组卷：164引用：24难度：0.7

  解析

• 2．下列图形中，既是轴对称图形又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：4引用：1难度：0.9

  解析

• 3．若x₁、x₂是一元二次方程x²-5x+6=0的两个根，则x₁+x₂+x₁•x₂的值是（　　）

  A．1

  B．11

  C．-11

  D．-1
  组卷：118引用：9难度：0.9

  解析

• 4．二次函数y=-3x²-6x+5的图象的顶点坐标是（　　）

  A．（1，8）

  B．（-1，8）

  C．（-1，2）

  D．（1，-4）
  组卷：687引用：81难度：0.9

  解析

• 5．如图，该图形围绕自己的旋转中心，按下列角度旋转后，不能与其自身重合的是（　　）

  A．72°

  B．108°

  C．144°

  D．216°
  组卷：1023引用：68难度：0.9

  解析

• 6．用配方法解方程x²-2x-5=0时，原方程变形为（　　）

  A．（x-1）2=6

  B．（x+1）2=6

  C．（x-2）2=9

  D．（x+2）2=9
  组卷：215引用：13难度：0.9

  解析

• 7．若（2，5）、（4，5）是抛物线y=ax²+bx+c上的两个点，则它的对称轴是（　　）

  A．x=- b a

  B．x=1

  C．x=2

  D．x=3
  组卷：5027引用：65难度：0.9

  解析

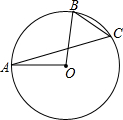• 8．如图，点A，B，C是⊙O上的三点，已知∠AOB=100°，那么∠ACB的度数是（　　）

  A．30°

  B．40°

  C．50°

  D．60°
  组卷：2357引用：67难度：0.9

  解析

五、解答题（每小题9分，共27分）

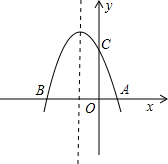• 24．如图，抛物线y=-x²+bx+c与x轴交于A（1，0），B（-3，0）两点．
  （1）求该抛物线的解析式；
  （2）设（1）中的抛物线交y轴于C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由．
  （3）在（1）中的抛物线上的第二象限上是否存在一点P，使△PBC的面积最大？若存在，求出△PBC面积的最大值．若没有，请说明理由．
  组卷：850引用：17难度：0.7

  解析

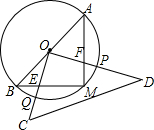• 25．如图，AB是⊙O的直径，

  AB

  =

  6

  2

  ，M是弧AB的中点，OC⊥OD，△COD绕点O旋转与△AMB的两边分别交于E、F（点E、F与点A、B、M均不重合），与⊙O分别交于P、Q两点．
  （1）求证：OE=OF；
  （2）连接PM、QM，试探究：在△COD绕点O旋转的过程中，∠PMQ是否为定值？若是，求出∠PMQ的大小；若不是，请说明理由；
  （3）连接EF，试探究：在△COD绕点O旋转的过程中，△EFM的周长是否存在最小值？若存在，求出其最小值；若不存在，请说明理由．
  组卷：651引用：6难度：0.5

  解析