2022-2023学年广东省江门市蓬江区九年级（上）第一次联考数学试卷
发布：2024/7/21 8:0:9
一、选择题：只有一项是符合题目要求的，本小题共10小题，每小题5分，共50分
-
1．实数abc在数轴上的对应点的位置如图所示，如果a+c=0，那么下列结论正确的是（ ）组卷：908引用：11难度：0.5 -
2．关于x的一元一次方程（k-1）x=4的解是整数，则符合条件的所有整数k的值的和是（ ）
组卷：844引用：4难度：0.7 -
3．化简x
，正确的是（ ）-1x组卷：1616引用：16难度：0.9 -
4．若10x=N，则称x是以10为底N的对数．记作：x=lgN．
例如：102=100，则2=lg100；100=1，则0=lg1．
对数运算满足：当M＞0，N＞0时，lgM+lgN=lg（MN）．
例如：lg3+lg5=lg15，则（lg5）2+lg5×lg2+lg2的值为（ ）组卷：1286引用：14难度：0.6 -
5．两个形状大小完全相同的长方形中放入4个相同的小长方形后，得到图①和图②的阴影部分，如果大长方形的长为m,则图②与图①的阴影部分周长之差是（ ）组卷：1626引用：10难度：0.5 -
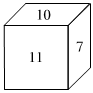6．一个正方体，六个面上分别写着六个连续的整数，且每个相对面上的两个数字之和相等，如图你能看到的数为7，10，11，则这六个整数的和可能为（ ）组卷：142引用：5难度：0.7 -
7．甲乙两地相距360千米，一轮船往返于甲、乙两地之间，顺水行船用18小时，逆水行船用24小时，若设船在静水中的速度为x千米/时，水流速度为y千米/时，则下列方程组中正确的是（ ）
组卷：4388引用：57难度：0.7
三、解答题本大题共6小题，共55分
-
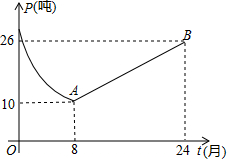22．某药厂销售部门根据市场调研结果，对该厂生产的一种新型原料药未来两年的销售进行预测，并建立如下模型：设第t个月该原料药的月销售量为P（单位：吨），P与t之间存在如图所示的函数关系，其图象是函数P=（0＜t≤8）的图象与线段AB的组合；设第t个月销售该原料药每吨的毛利润为Q（单位：万元），Q与t之间满足如下关系：Q=120t+42t+8，0＜t≤12-t+44，12＜t≤24
（1）当8＜t≤24时，求P关于t的函数解析式；
（2）设第t个月销售该原料药的月毛利润为w（单位：万元）
①求w关于t的函数解析式；
②该药厂销售部门分析认为，336≤w≤513是最有利于该原料药可持续生产和销售的月毛利润范围，求此范围所对应的月销售量P的最小值和最大值．组卷：3256引用：12难度：0.1 -
23．在线上教学中，教师和学生都学习到了新知识，掌握了许多新技能．例如教材八年级下册的数学活动--折纸，就引起了许多同学的兴趣．在经历图形变换的过程中，进一步发展了同学们的空间观念，积累了数学活动经验．
实践发现：
对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平；再一次折叠；纸片，使点A落在EF上的点N处，并使折痕经过点B，得到折痕BM，把纸片展平，连接AN，如图①．
（1）折痕BM （填“是”或“不是”）线段AN的垂直平分线；请判断图中△ABN是什么特殊三角形？答：；进一步计算出∠MNE=；
（2）继续折叠纸片，使点A落在BC边上的点H处，并使折痕经过点B，得到折痕BG，把纸片展平，如图②，则∠GBN=；
拓展延伸：
（3）如图③，折叠矩形纸片ABCD，使点A落在BC边上的点A'处，并且折痕交BC边于点T，交AD边于点S，把纸片展平，连接AA′交ST于点O，连接AT，SA′．求证：四边形SATA′是菱形．
解决问题：
（4）如图④，矩形纸片ABCD中，AB=10，AD=26，点S是边AD上的一动点，折叠纸片，使点A落在BC边上的点A′处，并且折痕过点S，交AB边于点T，把纸片展平．同学们小组讨论后，得出线段AT长度的取值范围，请你求出线段AT长度的取值范围．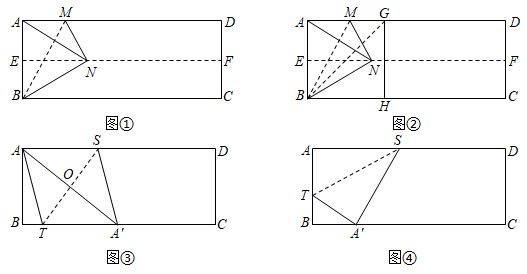
组卷：247引用：2难度：0.3
