在线上教学中，教师和学生都学习到了新知识，掌握了许多新技能．例如教材八年级下册的数学活动--折纸，就引起了许多同学的兴趣．在经历图形变换的过程中，进一步发展了同学们的空间观念，积累了数学活动经验．
实践发现：
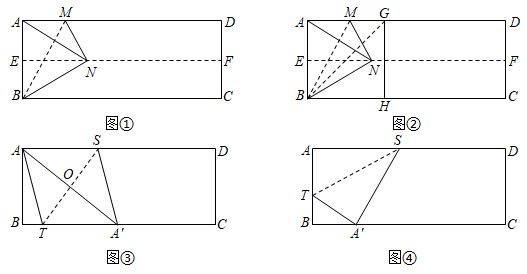
对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平；再一次折叠；纸片，使点A落在EF上的点N处，并使折痕经过点B，得到折痕BM，把纸片展平，连接AN，如图①．
（1）折痕BM 是是（填“是”或“不是”）线段AN的垂直平分线；请判断图中△ABN是什么特殊三角形？答：等边三角形等边三角形；进一步计算出∠MNE=60°60°；
（2）继续折叠纸片，使点A落在BC边上的点H处，并使折痕经过点B，得到折痕BG，把纸片展平，如图②，则∠GBN=15°15°；
拓展延伸：
（3）如图③，折叠矩形纸片ABCD，使点A落在BC边上的点A'处，并且折痕交BC边于点T，交AD边于点S，把纸片展平，连接AA′交ST于点O，连接AT，SA′．求证：四边形SATA′是菱形．
解决问题：
（4）如图④，矩形纸片ABCD中，AB=10，AD=26，点S是边AD上的一动点，折叠纸片，使点A落在BC边上的点A′处，并且折痕过点S，交AB边于点T，把纸片展平．同学们小组讨论后，得出线段AT长度的取值范围，请你求出线段AT长度的取值范围．
【考点】四边形综合题．
【答案】是；等边三角形；60°；15°
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/21 8:0:9组卷：247引用：2难度：0.3
相似题
-
1．[证明体验]
（1）如图1，在△ABC中，点D在边BC上，点F在边AC上，AB=AD，FB=FC，AD与BF相交于点E．求证：∠ABF=∠CAD．
[思考探究]
（2）如图2，在（1）的条件下，过点D作AB的平行线交AC于点G，若DE=2AE，AB=6，求DG的长．
[拓展延伸]
（3）如图3，在四边形ABCD中，对角线AC与BD相交于点O，AC⊥AD，∠ABC=∠ACB=67.5°，OD=2OB，OA=，求CD的长．2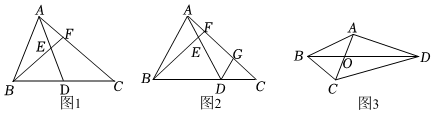
发布：2025/5/23 23:30:1组卷：687引用：3难度：0.3 -
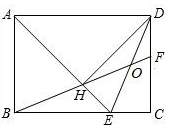2．如图，在矩形ABCD中，AD=AB，∠BAD的平分线交BC于点E．DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：①AD=AE；②∠AED=∠CED；③OE=OD；④BH=HF；⑤BC-CF=2HE，其中正确的有（ ）2发布：2025/5/23 22:30:2组卷：1273引用：4难度：0.2 -
3．【问题提出】
（1）如图①，OP为∠AOB的平分线，PC⊥OA于点C，PD⊥OB于点D，若S△OPC=3，则S△OPD=
【问题探究】
（2）如图②，a、b是两条平行的直线，且a、b之间的距离为12，点A为直线a上一点，点B、C为直线b上两点，且点B在点C的左侧，若∠BAC=45°，求BC的最小值；
【问题解决】
（3）如图③，四边形ABCD是园林规划局欲修建的一块平行四边形园林的大致示意图，沿对角线BD修一条人行走道，沿∠BAD的平分线AP（点P在BD上）修一条园林灌溉水渠．根据规划要求，∠ABC=120°，AP=120米，且使得平行四边形ABCD的面积尽可能小，问平行四边形ABCD的面积是否存在最小值？若存在，求出其最小值，若不存在，请说明理由．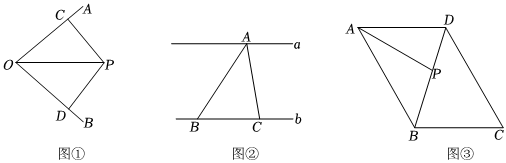
发布：2025/5/23 22:30:2组卷：137引用：1难度：0.2
