2022-2023学年重庆市沙坪坝区大学城四中七年级（下）第三次月考数学试卷

一、选择题：（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑．

• 1．下列数是无理数的有（　　）

  A． 2

  B．-1

  C．0

  D． 1 2
  组卷：190引用：4难度：0.7

  解析

• 2．点P（2，-3）所在的象限为（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：465引用：77难度：0.9

  解析

• 3．不等式x＜2的解集在数轴上可表示为（　　）

  A．

  B．

  C．

  D．
  组卷：235引用：2难度：0.9

  解析

• 4．为了解七年级4000名学生参加数学统测成绩的情况，从中随机抽取200名学生的数学成绩进行分析．下列说法正确的是（　　）

  A．样本容量是200名

  B．每名学生是个体

  C．200名学生的数学成绩是总体的一个样本

  D．4000名学生是总体
  组卷：93引用：2难度：0.9

  解析

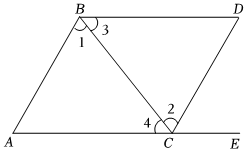• 5．如图，点E在AC的延长线上，下列条件中能判断AB∥CD的是（　　）

  A．∠3=∠4	B．∠1=∠2
  C．∠D=∠DCE	D．∠D+∠DCA=180°
  组卷：1775引用：54难度：0.7

  解析

• 6．估算

  72

  的值（　　）

  A．在6和7之间	B．在7和8之间
  C．在8和9之间	D．在9和10之间
  组卷：104引用：2难度：0.8

  解析

• 7．下列语句：①在同一平面内，若三条直线只有两个交点，则其中两条直线互相平行；②如果两条平行线被第三条所截，同旁内角相等，那么这两条平行线都与第三条直线垂直；③过一点有且只有一条直线与已知直线平行，其中（　　）

  A．①②是真命题	B．②③是真命题
  C．①③是真命题	D．以上结论皆是假命题
  组卷：130引用：5难度：0.7

  解析

• 8．《九章算术》中记载：今有共买物，人出八，盈三；人出七，不足四，问人数、物价各几何？现有一类似问题：今有人组团购一物，如果每人出10元，则多了6元；如果每人出8元，则少了8元，问组团人数和物价各是多少？若设x人参与组团，物价为y元，则以下列出的方程组正确的是（　　）

  A． 10 x - y = 6 8 x - y = 8	B． y - 10 x = 6 y - 8 x = 8
  C． 10 x - y = 6 y - 8 x = 8	D． y - 10 x = 6 8 x - y = 8
  组卷：172引用：5难度：0.6

  解析

四、解答题：（本大题6个小题，21-25每小题10分，26题12分，共62分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上．

• 25．随着“低碳生活，绿色出行”理念的普及，新能源汽车正逐渐成为人们喜爱的交通工具．某汽车销售公司计划购进一批新能源汽车进行销售，据了解2辆A型汽车、3辆B型汽车的进价共计65万元；3辆A型汽车、1辆B型汽车的进价共计45万元．
  （1）求A、B两种型号的汽车每辆进价分别为多少万元？
  （2）“五一劳动节”前夕，该公司用不超过105万元购进A、B两型汽车各若干辆，其中A型汽车数量是B型数量的2倍，请你通过计算设计共有哪几种购买方案．
  （3）在（2）条件下，选择购车数量最多购车方案，公司决定把A型汽车的进价提高40%作为定价，把B型汽车的进价提高20%作为定价，并决定从5月1号到5月3号三天小长假期间，对A、B两型汽车进行打折促销，以定价为基础，A型车打m折销售，每辆B型车降价

  m

  +

  10

  .

  5

  10

  万元销售．除了汽车进价，销售A、B两型汽车每天还需要支出1万元的其他费用．经过促销，三天假期结束时，该公司销售完“五一节”前夕购进的A、B两型汽车，共获利19.8万元，求m的值．
  组卷：110引用：1难度：0.6

  解析

• 26．如图1，直线MN∥PQ，直线AB分别交MN、PQ于A、B点，∠ABP＜90°，点D在线段BQ上（不在端点处），点C在直线AB上，点E在直线MN上，连接CD、CE．
  
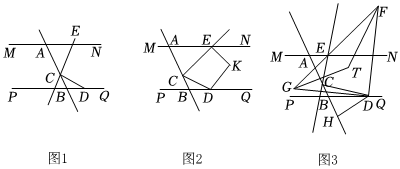
  （1）如图1，点C在线段AB上，若EC⊥CD，∠AEC=65°，则∠CDB的度数为

  ；
  （2）如图2，点C在线段AB上，点K为直线MN与PQ之间区域的一点，点E在线段AN上（不与端点重合），连EK、KD．若∠ECD=60°，∠NEK=

  1

  3

  ∠CEN，∠KDQ=

  1

  3

  ∠CDQ，求∠EKD的度数；
  （3）如图3，DH⊥AB于点H，EC⊥CD，点C在射线HA上运动（C不与H重合），∠AEC与∠CDB的角平分线所在直线交于点G，∠AEC与∠CDQ的角平分线所在直线交于点F，∠FGD与∠GFD的角平分线交于点T，直接写出∠FEN、∠CDG与∠FGT的数量关系．
  组卷：306引用：1难度：0.2

  解析