当前位置：试卷中心 > 试卷详情

2022-2023学年山东省日照市五莲县七年级（下）期末数学试卷

发布：2024/7/5 8:0:9

一、选择题：本大题共12个小题；每小题3分，满分36分.在每小题给出的四个选项中，只有一项是正确的，请将正确选项的字母代号涂在答题卡相应位置上。

1．在
-
3
2
，
-
4
，0.
•
2
•
3
，
π
3
中，无理数为（　　）
A．
-
3
2
B．
-
4
C．0.
•
2
•
3
D．
π
3
组卷：193引用：4难度：0.8
解析
2．已知a＞b,下列变形一定正确的是（　　）
A．5a＜5b B．2-a＞2-b C．1+2a＞1+2b D．ac²＞bc²
组卷：326引用：3难度：0.7
解析
3．下列说法中，错误的是（　　）
A．8的立方根是±2
B．4的算术平方根是2
C．
81
的平方根是±3
D．立方根等于-1的实数是-1
组卷：1834引用：13难度：0.7
解析
4．某中学为了了解学校520名学生的睡眠情况，抽查了其中100名学生的睡眠时间进行统计，下列叙述正确的是（　　）
A．以上调查属于全面调查
B．100名学生是总体的一个样本
C．520是样本容量
D．每名学生的睡眠时间是一个个体
组卷：189引用：7难度：0.9
解析
5．已知点P位于y轴左侧，距y轴3个单位长度，位于x轴上方，距离x轴4个单位长度，则点P的坐标是（　　）
A．（-3，4） B．（3，-4） C．（-4，3） D．（4，-3）
组卷：153引用：3难度：0.9
解析
6．如图，小聪把一块含有60°角的直角三角形板的两个顶点放在直尺的对边上，并测得∠1=25°，则∠2的度数是（　　）
A．25° B．30° C．35° D．60°
组卷：1094引用：19难度：0.9
解析
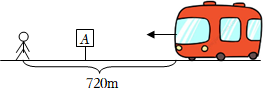7．如图，小明想到A站乘公交车，发现他与公交车的距离为720m.假设公交车的速度是小明速度的5倍．若要保证小明不会错过这辆公交车，则小明到A站之间的距离最大为（　　）
A．100m B．120m C．180m D．144m
组卷：882引用：8难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题：本大题共6小题；共68分。解答应写出文字说明，证明过程或演算步骤

21．某旅游商品经销店欲购进A、B两种纪念品，若用380元购进A种纪念品7件，B种纪念品8件；也可以用380元购进A种纪念品10件，B种纪念品6件．
（1）求A、B两种纪念品的进价分别为多少？
（2）若该商店每销售1件A种纪念品可获利5元，每销售1件B种纪念品可获利7元，该商店准备用不超过900元购进A、B两种纪念品40件，且这两种纪念品全部售出后总获利不低于216元，有哪几种进货方案？
（3）通过计算说明：在（2）问的前提下应该怎样进货，才能使总获利最大？
组卷：228引用：4难度：0.5
解析
22．【阅读理解】
我们经常过某个点作已知直线的平行线，以便利用平行线的性质来解决问题．
例如：如图1，AB∥CD，点E、F分别在直线AB、CD上，点P在直线AB、CD之间，设∠AEP=∠α，∠CFP=∠β，求证：∠P=∠α+∠β．
证明：如图2，过点P作PQ∥AB，
∴∠EPQ=∠AEP=∠α，
∵PQ∥AB，AB∥CD，
∴PQ∥CD，
∴∠FPQ=∠CFP=∠β，
∴∠EPF=∠EPQ+∠FPQ=∠α+∠β．
即∠P=∠α+∠β．
可以运用以上结论解答下列问题：
【类比应用】
（1）如图3，已知AB∥CD，已知∠D=40°，∠GAB=60°，求∠P的度数；
（2）如图4，已知AB∥CD，点E在直线CD上，点P在直线AB上方，连接PA、PE．设∠A=∠α、∠CEP=∠β，则∠α、∠β、∠P之间有何数量关系？请说明理由；
【拓展应用】
（3）如图5，已知AB∥CD，点E在直线CD上，点P在直线AB上方，连接PA、PE，∠PED的角平分线与∠PAB的角平分线所在直线交于点Q，求
1
2
∠
P
+
∠
Q
的度数．
组卷：388引用：4难度：0.6
解析