【阅读理解】
我们经常过某个点作已知直线的平行线,以便利用平行线的性质来解决问题.
例如:如图1,AB∥CD,点E、F分别在直线AB、CD上,点P在直线AB、CD之间,设∠AEP=∠α,∠CFP=∠β,求证:∠P=∠α+∠β.
证明:如图2,过点P作PQ∥AB,
∴∠EPQ=∠AEP=∠α,
∵PQ∥AB,AB∥CD,
∴PQ∥CD,
∴∠FPQ=∠CFP=∠β,
∴∠EPF=∠EPQ+∠FPQ=∠α+∠β.
即∠P=∠α+∠β.
可以运用以上结论解答下列问题:
【类比应用】
(1)如图3,已知AB∥CD,已知∠D=40°,∠GAB=60°,求∠P的度数;
(2)如图4,已知AB∥CD,点E在直线CD上,点P在直线AB上方,连接PA、PE.设∠A=∠α、∠CEP=∠β,则∠α、∠β、∠P之间有何数量关系?请说明理由;
【拓展应用】
(3)如图5,已知AB∥CD,点E在直线CD上,点P在直线AB上方,连接PA、PE,∠PED的角平分线与∠PAB的角平分线所在直线交于点Q,求12∠P+∠Q的度数.
1
2
∠
P
+
∠
Q
【答案】(1)∠P=100°;(2)∠P=∠α+∠β-180°,理由见解析;(3)180°.
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/7/5 8:0:9组卷:388引用:4难度:0.6
相似题
-
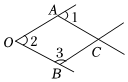 1.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,∠ACB的度数,并说明理由.
1.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,∠ACB的度数,并说明理由.
解:OA∥BC,OB∥AC.
理由:∵∠1=50°,∠2=50°,
∴∠1=∠2(等量代换)
∴OB∥AC. ( ),
∴∠3+∠ACB=180°,( ),
∴∠ACB=°,
∵∠2=50°,∠3=130°,
∴∠2+∠3=180°,
∴OA∥BC.( ).发布:2025/6/7 21:0:1组卷:680引用:6难度:0.9 -
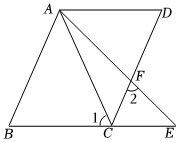 2.如图,已知AB∥CD,∠B=∠D.
2.如图,已知AB∥CD,∠B=∠D.
(1)求证:AD∥BE;
(2)若∠1=∠2=60°,∠BAC=3∠EAC,求∠DAF的度数.发布:2025/6/7 20:30:1组卷:277引用:6难度:0.7 -
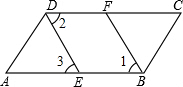 3.如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,DE∥FB.求证:AB∥DC.
3.如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,DE∥FB.求证:AB∥DC.
请根据条件进行推理,得出结论,并在括号内注明理由.
证明:∵BF、DE分别平分∠ABC与∠ADC,
∴∠1=∠ABC,∠2=12∠ADC.(12)
∵∠ABC=∠ADC,
∴.
∵DE∥FB
∴∠1=∠3,()
∴∠2=.(等量代换)
∴AB∥CD.()发布:2025/6/7 21:30:1组卷:637引用:4难度:0.3


