2022-2023学年山东省泰安市岱岳区七年级（下）期末数学试卷（五四学制）
发布：2024/6/28 8:0:9
一、选择题（本大题共16小题，在每小题给出的四个选项中，只有一个是正确的，请把正确的选项选出来，每小题选对得3分，选错、不选或选出的答案超过一个，均记零分）
-
1．若x＞y,则下列不等式一定成立的是（ ）
组卷：229引用：6难度：0.8 -
2．由x-
可以得到用x表示y的式子为（ ）y2=1组卷：92引用：2难度：0.8 -
3．如图，下列条件中不能判定AB∥CD的是（ ）组卷：127引用：4难度：0.7 -
4．某日我市最高气温是25℃，最低气温是12℃，则当天气温t（℃）的变化范围是（ ）
组卷：462引用：5难度：0.9 -
5．如图，在△ABC与△EBF中，若AB=BE，BC=BF，要使这两个三角形全等，还需具备的条件是（ ）组卷：255引用：1难度：0.7 -
6．将一粒大豆抛在印有正方体小方格的桌面上，大豆落在阴影区域的概率是（ ）组卷：41引用：1难度：0.6 -
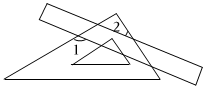7．将一把直尺与一块直角三角板按如图所示的方式放置，若∠1=125°，则∠2的度数为（ ）组卷：232引用：5难度：0.7 -
8．若
是关于x,y的方程2x-3y-4a=0的一个解，则常数a为（ ）x=5y=-2组卷：226引用：3难度：0.7 -
9．如图，三角形ABC中，∠ACB=90°，CD是高，∠A=30°，AB=8，则BD的长为（ ）组卷：311引用：3难度：0.7
三、解答题（本大题共7小题，满分78分，解答应写出必菱的文字说明、证明过程或演步骤）
-
28．在平面直角坐标系中，O是坐标原点，直线OA、BA相交于点A，A点坐标（3，4），B点坐标（-1，0）．
（1）分别求直线OA、BA的表达式；
（2）作x轴的垂线分别交直线OA，BA于点M（x,m），N（x,n），当0＜m＜n时，求x的取值范围；
（3）求△AOC的面积；
（4）P是x轴上的一个点，当△AOP是等腰三角形时，直接写出P点的坐标．组卷：271引用：1难度：0.5 -
29．小明在学习了“命题”“逆命题”相关知识后发现有的平面图形的判定方法，是通过研究其性质定理的逆命题得出的，在学习等腰三角形的相关知识时，小明发现其性质定理“等边对等角”与判定定理“等角对等边”也存在互逆关系，如图1，用几何语言表达就是：
性质：∵AB=AC，
∴∠B=∠C，
判定：∵∠B=∠C，
∴AB=AC．
由此，爱动脑筋的小明进行了如下思考：“等腰三角形三线合一”的性质可以分解为三个不同的真命题，即：
（1）等腰三角形底边上的中线也是底边上的高线；
（2）等腰三角形顶角的平分线也是底边上的高线：
（3）等腰三角形顶角的平分线也是底边上的中线；
由此3个真命题，小明得到三个新命题，即：
Ⅰ．如果一个三角形一边上的中线也是这边上的高线，那么这个三角形是等腰三角形；
Ⅱ．如果一个三角形一个角的平分线也是这个角对边上的高线，那么这个三角形是等腰三角形；
Ⅲ． ．
（1）请你根据前面的命题3写出小明猜想的第Ⅲ个命题：；
（2）小明认为这三个命题如果是真命题，那么就可以作为等腰三角形的判定方法，于是小明对三个命题进行证明，他把前两个命题根据图2写出了已知，求证：
命题Ⅰ：△ABC中，D是BC边上的中点，AD⊥BC，求证：△ABC是等腰三角形；
命题Ⅱ：△ABC中，AD平分∠BAC，AD⊥BC，求证：△ABC是等腰三角形；
命题Ⅲ：；
①请你写出命题Ⅲ的几何语言；
②小明猜想的三个命题是否都是真命题，如果不是，请说明理由．如果是，请帮助小明进行证明．
组卷：105引用：1难度：0.3
