2022-2023学年广东省东莞实验中学高二（上）月考数学试卷（一）

一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知

  a

  、

  b

  都是空间向量，且＜

  a

  ，

  b

  ＞=

  2

  π

  3

  ，则＜2

  a

  ，-3

  b

  ＞=（　　）

  A． π 3

  B． π 6

  C． 2 π 3

  D． 5 π 6
  组卷：59引用：8难度：0.8

  解析

• 2．经过A（-2，0），B（-2，3）两点的直线的倾斜角是（　　）

  A．45°

  B．60°

  C．90°

  D．135°
  组卷：207引用：6难度：0.8

  解析

• 3．已知空间向量

  a

  ，

  b

  ，

  c

  ，则下列说法正确的是（　　）

  A．若 a ∥ b ， b ∥ c ，则 a ∥ c	B．若 | a • b | = | a | • | b | ，则 a 与 b 共线
  C．若 a • c = b • c ，则 a = b	D． （ a • b ） • c = （ b • c ） • a
  组卷：57引用：8难度：0.7

  解析

• 4．设点

  A

  （

  1

  ，-

  1

  ，

  2

  ）

  关于坐标原点的对称点是B，则|AB|等于（　　）

  A．4

  B． 2 3

  C． 2 2

  D．2
  组卷：109引用：6难度：0.8

  解析

• 5．已知

  a

  =（-2，1，3），

  b

  =（-1，2，1），若

  a

  ⊥（

  a

  -λ

  b

  ），则实数λ的值为（　　）

  A．-2

  B． - 14 3

  C． 14 5

  D．2
  组卷：368引用：44难度：0.9

  解析

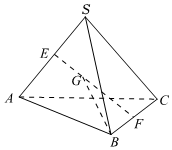• 6．如图，在三棱锥S-ABC中，点E，F分别是SA，BC的中点，点G满足

  EG

  =

  1

  3

  EF

  ，若

  SA

  =

  a

  ，

  SB

  =

  b

  ，

  SC

  =

  c

  ，则

  BG

  =（　　）

  A． 1 3 a + 5 6 b + 1 6 c	B． 1 3 a - 5 6 b + 1 6 c
  C． - 1 3 a - 1 6 b + 1 2 c	D． 1 3 a - 1 6 b + 1 2 c
  组卷：389引用：8难度：0.7

  解析

• 7．在二面角的棱上有两个点A、B，线段AC、BD分别在这个二面角的两个面内，并且都垂直于棱AB，若AB=1，AC=2，BD=3，CD=2

  2

  ，则这个二面角的大小为（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  组卷：616引用：6难度：0.5

  解析

四、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．空间中，两两互相垂直且有公共原点的三条数轴构成直角坐标系，如果坐标系中有两条坐标轴不垂直，那么这样的坐标系称为“斜坐标系”．现有一种空间斜坐标系，它任意两条数轴的夹角均为60°，我们将这种坐标系称为“斜60°坐标系”．我们类比空间直角坐标系，定义“空间斜60°坐标系”下向量的斜60°坐标：

  i

  ，

  j

  ，

  k

  分别为“斜60°坐标系”下三条数轴（x轴、y轴、z轴）正方向的单位向量，若向量

  n

  =

  x

  i

  +

  y

  j

  +

  z

  k

  ，则

  n

  与有序实数组（x,y,z）相对应，称向量

  n

  的斜60°坐标为[x,y,z]，记作

  n

  =

  [

  x

  ,

  y

  ,

  z

  ]

  ．
  （1）若

  a

  =

  1 ， 2 ， 3

  ，

  b

  =

  [

  -

  1

  ，

  1

  ，

  2

  ]

  ，求

  a

  +

  b

  的斜60°坐标；
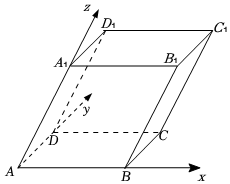
  （2）在平行六面体ABCD-ABC₁D₁中，AB=AD=2，AA₁=3，∠BAD=∠BAA₁=∠DAA₁=60°，如图，以

  {

  AB

  ，

  AD

  ，

  A

  A

  1

  }

  为基底建立“空间斜60°坐标系”．
  ①若

  BE

  =

  EB

  1

  ，求向量

  ED

  1

  的斜60°坐标；
  ②若

  AM

  =

  [

  2

  ，

  t

  ,

  0

  ]

  ，且

  AM

  ⊥

  A

  C

  1

  ，求

  |

  AM

  |

  ．
  组卷：292引用：12难度：0.6

  解析

• 22．在三棱柱ABC-A₁B₁C₁中，侧面正方形BB₁C₁C的中心为点M，A₁M⊥平面BB₁C₁C，且

  B

  B

  1

  =

  2

  ，

  AB

  =

  3

  ，点E满足

  A

  1

  E

  =

  λ

  A

  1

  C

  1

  （

  0

  ≤

  λ

  ≤

  1

  ）

  ．
  
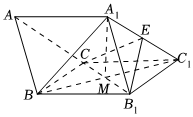
  （1）若A₁B∥平面B₁CE，求λ的值；
  （2）求点E到平面ABC的距离；
  （3）若平面ABC与平面B₁CE所成角的正弦值为

  2

  5

  5

  ，求λ的值．
  组卷：14引用：4难度：0.5

  解析