2022-2023学年辽宁省本溪高级中学高三（上）期中数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．设全集U=R，集合A={x|x²≥4}，B={x|-4≤x≤1}，则（∁_UA）∩B=（　　）

  A．{x|-2＜x≤1}

  B．{x|-4≤x＜2}

  C．{x|x＜2}

  D．{x|-4≤x≤1}
  组卷：17引用：4难度：0.8

  解析

• 2．若命题p：∀x≥1，x³≥1，则￢p为（　　）

  A．∀x≥1，x3＜1

  B．∀x＜1，x3＜1

  C．∃x≥1，x3＜1

  D．∃x＜1，x3＜1
  组卷：5引用：2难度：0.9

  解析

• 3．已知复数z满足z（1-i）=3-i,则

  z

  •

  z

  =（　　）

  A．5

  B． 10

  C． 2 2

  D．2
  组卷：112引用：7难度：0.7

  解析

• 4．手机屏幕面积与整机面积的比值叫手机的“屏占比”，它是手机外观设计中一个重要参数，其值通常在（0，1）之间．设计师将某手机的屏幕面积和整机面积同时增加相同的数量，升级为一款新的手机外观，则该手机“屏占比”和升级前比有什么变化（　　）

  A．“屏占比”不变	B．“屏占比”变小
  C．“屏占比”变大	D．变化不确定
  组卷：220引用：10难度：0.8

  解析

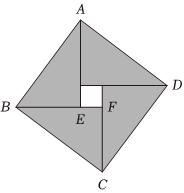• 5．我国勾股定理最早的证明是东汉末期数学家赵爽在为《周髀算经》作注时给出的赵爽弦图（如图），它是由四个全等的直角三角形拼成的内、外都是正方形的美丽图案．若BF=3EF=3，则

  （

  AE

  -

  FE

  -

  CF

  ）

  •

  BC

  =（　　）

  A．9

  B．13

  C．18

  D．2
  组卷：21引用：2难度：0.8

  解析

• 6．把函数y=f（x）图像上所有点的横坐标缩短到原来的

  1

  2

  倍，纵坐标不变，再把所得曲线向右平移

  π

  3

  个单位长度，得到函数y=sin（x-

  π

  4

  ）的图像，则f（x）=（　　）

  A．sin（ x 2 - 7 π 12 ）	B．sin（ x 2 + π 12 ）
  C．sin（2x- 7 π 12 ）	D．sin（2x+ π 12 ）
  组卷：8522引用：39难度：0.8

  解析

• 7．在三棱锥M-ABC中，MA⊥平面ABC，△ABC是边长为2的正三角形，MA=2

  3

  ，E，F分别为MA，MC的中点，则异面直线BE与AF所成角的余弦值为（　　）

  A． 42 7

  B． 7 7

  C． 10 5

  D． 4 70 35
  组卷：22引用：2难度：0.5

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤。

• 21．已知等轴双曲线

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的一个焦点为

  F

  （

  2

  ，

  0

  ）

  ．
  （1）求双曲线C的方程；
  （2）已知点A是C上一定点，过点B（0，1）的动直线与双曲线C交于P，Q两点，若k_AP+k_AQ为定值λ，求点A的坐标及实数λ的值．
  组卷：92引用：3难度：0.5

  解析

• 22．已知函数f（x）=2e^x-x²-ax-2，当x≥0时，f（x）≥0．
  （1）求a的取值范围；
  （2）求证：

  （

  1

  +

  2

  2

  e

  -

  1

  ）

  （

  1

  +

  2

  2

  e

  2

  -

  1

  ）

  （

  1

  +

  2

  2

  e

  3

  -

  1

  ）

  …

  （

  1

  +

  2

  2

  e

  n

  -

  1

  ）

  ＜

  4

  （n∈N^*）．
  组卷：24引用：2难度：0.5

  解析