2022-2023学年山东省枣庄十八中高一（下）月考数学试卷（6月份）

一、单项选择题：本题共7小题，每小题5分，共35分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．复数z满足

  z

  •（1+2i）=4+3i,则z等于（　　）

  A．2-i

  B．2+i

  C．1+2i

  D．1-2i
  组卷：86引用：9难度：0.9

  解析

• 2．某工厂生产甲、乙、丙三种型号的产品，产品数量之比为2：3：5，现按型号用分层抽样的方法随机抽出容量为n的样本，若抽到24件乙型产品，则n等于（　　）

  A．80

  B．70

  C．60

  D．50
  组卷：102引用：9难度：0.9

  解析

• 3．已知

  a

  =

  （

  sin

  15

  °

  ，

  sin

  75

  °

  ）

  ，

  b

  =

  （

  cos

  30

  °

  ，

  sin

  30

  °

  ）

  ，则

  a

  •

  b

  =（　　）

  A． 2 2

  B． - 2 2

  C． 1 2

  D． - 1 2
  组卷：174引用：4难度：0.8

  解析

• 4．有一组样本数据x₁，x₂，…，x_n，由这组数据得到的另一组数据y₁，y₂，…，y_n，满足y_i=-x_i+c（c为非零常数），则下列结论一定成立的是（　　）

  A．两组数据的样本平均数不同

  B．两组数据的中位数相同

  C．两组数据的样本方差相同

  D．两组数据的样本标准差不同
  组卷：189引用：5难度：0.8

  解析

• 5．已知α，β是两个不同的平面，m,n是两条不同的直线，下列四个命题中正确的是（　　）

  A．如果m∥α，n∥α，那么m∥n

  B．如果m⊥α，n∥α，那么m⊥n

  C．如果m⊥n,m⊥α，n∥β，那么α⊥β

  D．如果α∥β，直线m与α所成的角和直线n与β所成的角相等，那么m∥n
  组卷：97引用：8难度：0.7

  解析

四、解答题：本题共4小题，共70分，解答应写出文字说明，证明过程或演算步骤。

• 16．在①

  b

  2

  +

  2

  ac

  =

  a

  2

  +

  c

  2

  ，②acosB=bsinA，③

  sin

  B

  +

  cos

  B

  =

  2

  ，这三个条件中任选一个，补充在下面的横线中，并解决该问题．已知△ABC中，_______，

  A

  =

  π

  3

  ，

  b

  =

  2

  ．
  （1）求角B；
  （2）求△ABC的面积．
  组卷：16引用：3难度：0.6

  解析

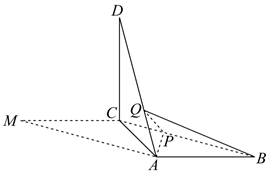• 17．如图，在平行四边形ABCM中，AB=AC=3，∠ACM=90°，以AC为折痕将△ACM折起，使点M到达点D的位置，且AB⊥DA．
  （1）证明：平面ACD⊥平面ABC；
  （2）Q为线段AD上一点，P为线段BC上一点，且BP=DQ=

  2

  3

  DA．
  ①求三棱锥Q-ABP的体积；
  ②求二面角Q-AP-C的余弦值．
  组卷：204引用：5难度：0.5

  解析