2022-2023学年黑龙江省哈尔滨市松北区顺迈学校七年级（上）段考数学试卷（12月份）（五四学制）

一、选择题（每题3分，共30分）

• 1．下列方程是一元一次方程的是（　　）

  A．4x+2y=3

  B．y+5=0

  C．x2=2x-1

  D． 1 y +y=2
  组卷：46引用：4难度：0.9

  解析

• 2．下列几组图形中，通过平移后能够重合的是（　　）

  A．

  B．

  C．

  D．
  组卷：128引用：5难度：0.5

  解析

• 3．下列实数中，属于无理数的是（　　）

  A． 22 7

  B．3.14

  C． 2

  D． 3 8
  组卷：409引用：13难度：0.7

  解析

• 4．在平面直角坐标系中，A（-2，6）在第（　　）象限．

  A．一

  B．二

  C．三

  D．四
  组卷：11引用：3难度：0.8

  解析

• 5．下列变形正确的是（　　）

  A．若2x=3，则x= 2 3	B．若-2x=6，则x=8
  C．若ma=mb,则a=b	D．若 a m = b m ，则a=b
  组卷：714引用：4难度：0.6

  解析

• 6．下列四个图形中，∠1与∠2互为内错角的是（　　）

  A．

  B．

  C．

  D．
  组卷：1223引用：9难度：0.6

  解析

• 7．甲、乙两班共有98人，若从甲班调3人到乙班，那么两班人数正好相等．设甲班原有人数是x人，可列出方程（　　）

  A．98+x=x-3	B．98-x=x-3
  C．（98-x）+3=x	D．（98-x）+3=x-3
  组卷：1738引用：46难度：0.9

  解析

• 8．在坐标平面中，把点A（-2，1）向右平移3个单位长度，再向上平移2个单位长度得到对应点B，则对应点B的坐标是（　　）

  A．（3，1）

  B．（-1，-3）

  C．（1，3）

  D．（-3，-1）
  组卷：338引用：5难度：0.6

  解析

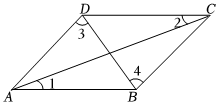• 9．如图，由AD∥BC可以得到的是（　　）

  A．∠1=∠2	B．∠3+∠4=90°
  C．∠DAB+∠ABC=180°	D．∠ABC+∠BCD=180°
  组卷：93引用：4难度：0.8

  解析

三、解答题（其中21-22题各7分，23-24题各8分，25-27题各10分，共60分）

• 26．已知，AB∥CD，F、G分别为直线AB、CD上的点，E为平面内任意一点，连接EF、EG．
  
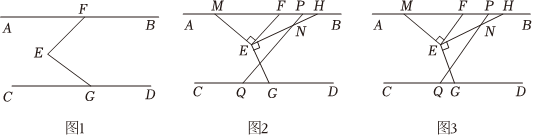
  （1）如图1，请直接写出∠AFE、∠CGE与∠FEG之间的数量关系．
  （2）如图2，过点E作EM⊥EF、EH⊥EG交直线AB上的点M、H，点N在EH上，过N作PQ∥EF，求证：∠HNQ=∠MEG．
  （3）如图3，在（2）的条件下，若∠ENQ=∠EMF，∠EGD=110°，求∠CQP的度数．
  组卷：83引用：2难度：0.7

  解析

• 27．在平面直角坐标系中，点A（m,n），C（n,0），且m、n满足

  m

  +

  1

  +

  （

  n

  -

  3

  ）

  2

  =

  0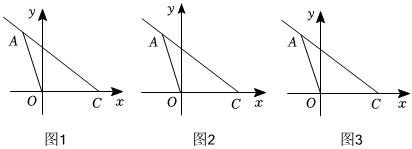

  ．
  
  （1）请直接写出A、C两点坐标；
  （2）若点P以每秒2个单位的速度从点C出发在射线CA上运动，若AC=5，点P的运动时间为t秒，请用含t的代数式表示线段AP的长度d（不必写出t的取值范围）；
  （3）在（2）的条件下，在点P运动的同时，点Q从点O出发，以每秒1个单位的速度沿x轴负半轴运动，连接OP、AQ，是否存在某一时刻，使S_△AOQ=2S_△AOP，若存在，请求出t值，并写出Q点坐标；若不存在，请说明理由．
  组卷：30引用：2难度：0.3

  解析