2022-2023学年山东省烟台市莱州一中高二（下）第二次质检数学试卷（6月份）

一、单选题（本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．）

• 1．函数

  f

  （

  x

  ）

  =

  2 x ， x ≥ 0

  f （ x + 3 ） ， x ＜ 0

  ，则f（-8）=（　　）

  A．4

  B．2

  C．8

  D．6
  组卷：9引用：5难度：0.8

  解析

• 2．设函数 f（x）=x²+ax,且

  lim

  △

  x

  →

  0

  f

  （

  1

  +

  △

  x

  ）

  -

  f

  （

  1

  ）

  △

  x

  =

  1

  ，则a=（　　）

  A． - 2 3

  B． - 3 2

  C．1

  D．-1
  组卷：987引用：7难度：0.8

  解析

• 3．已知函数f（x-1）=x²-2x,且f（a）=3，则实数a的值等于（　　）

  A． 2

  B． ± 2

  C．2

  D．±2
  组卷：258引用：4难度：0.9

  解析

• 4．下列求导运算正确的是（　　）

  A．（lnx+ 3 x ）′= 1 x + 3 x 2

  B．（x2ex）′=2xex

  C．（3xcos2x）′=3x（ln3•cos2x-2sin2x）

  D． （ ln 1 2 + lo g 2 x ） ′ = 2 + 1 xln 2
  组卷：231引用：5难度：0.7

  解析

• 5．“0＜a＜4”是“函数f（x）=

  1

  a

  x

  2

  -

  ax

  +

  1

  的定义域为R”的（　　）

  A．必要不充分条件	B．充分不必要条件
  C．充要条件	D．既不充分也不必要条件
  组卷：97引用：6难度：0.8

  解析

• 6．若直线y=x与曲线y=e^2x+m（m∈R，e为自然对数的底数）相切，则m=（　　）

  A．-2

  B．-1-ln2

  C．-ln2

  D．2
  组卷：211引用：3难度：0.7

  解析

• 7．已知函数f（x）与其导函数f'（x）的图象如图所示，则函数g（x）=

  f

  （

  x

  ）

  e

  x

  的单调递减区间为（　　）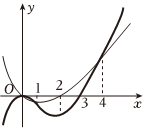

  A．（0，1）和（4，+∞）	B．（0，2）
  C．（-∞，0）和（1，4）	D．（0，3）
  组卷：288引用：2难度：0.4

  解析

四、解答题（本题共6小题，共70分，其中第17题10分，其它每题12分，解答应写出文字说明、证明过程或演算步骤．）

• 21．已知函数

  f

  （

  x

  ）

  =

  e x - 1 ， x ≥ 0

  1 2 a x 2 - ax , x ＜ 0

  ，其中a≠0．
  （1）若f（x）在R上单调递增，求实数a的取值范围；
  （2）对∀x₂＞0，∃x₁，使得f（x₁）=f（x₂），且x₁+x₂＜0，求实数a的取值范围．
  组卷：194引用：4难度：0.3

  解析

• 22．已知函数f（x）=lnx-x+2sinx.
  （1）证明：f（x）在区间（0，

  π

  2

  ）存在唯一的极值点；
  （2）试讨论f（x）的零点个数．
  组卷：154引用：2难度：0.4

  解析