2023-2024学年黑龙江省哈尔滨工业大学附中高二(上)开学数学试卷
发布:2024/7/29 8:0:9
一、单项选择题:(共8小题,每小题5分,共40分)
-
1.某中学高一年级有280人,高二年级有320人,为了解该校高一高二学生对暑假生活的规划情况,现用比例分配的分层随机抽样方法抽取一个容量为60的样本,则高一年级应抽取的人数为( )
组卷:152引用:3难度:0.9 -
2.已知i为虚数单位,若复数
=a+bi(a,b∈R),则a+b=( )1+i1-i组卷:148引用:9难度:0.9 -
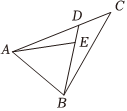 3.如图,点D为△ABC的边AC上靠近点C的三等分点,,设DE=14DB,AB=a,则AC=b=( )AE组卷:318引用:7难度:0.7
3.如图,点D为△ABC的边AC上靠近点C的三等分点,,设DE=14DB,AB=a,则AC=b=( )AE组卷:318引用:7难度:0.7 -
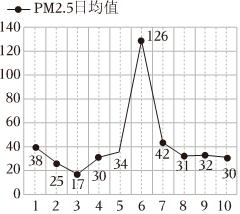 4.PM2.5是衡量空气质量的重要指标,如图是某地6月1日至10日的PM2.5日均值(单位:μg/m3)的折线图,则下列关于这10天中PM2.5日均值的说法错误的是( )组卷:44引用:3难度:0.7
4.PM2.5是衡量空气质量的重要指标,如图是某地6月1日至10日的PM2.5日均值(单位:μg/m3)的折线图,则下列关于这10天中PM2.5日均值的说法错误的是( )组卷:44引用:3难度:0.7 -
5.△ABC的三个内角A,B,C的对边分别为a,b,c,若a=2ccosB,
,则△ABC的形状是( )ccosB+bcosC=2c组卷:84引用:4难度:0.6 -
6.已知正三棱柱ABC-A1B1C1的所有棱长都是2,点M在棱CC1上运动,则A1M+BM的最小值为( )
组卷:33引用:3难度:0.7 -
7.已知△ABC的外接圆圆心为O,且
,2AO=AB+AC,则向量|OA|=|AC|在向量BA上的投影向量为( )BC组卷:103引用:4难度:0.5
四、解答题(本题共6小题,共70分.)
-
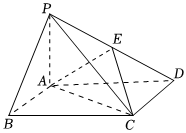 21.如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
21.如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(1)证明:PB∥平面AEC;
(2)设三棱锥E-ACD的体积是,AP=1,AD=38,求平面DAE与AEC的夹角.3组卷:60引用:7难度:0.6 -
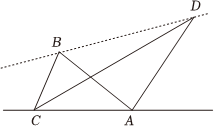 22.如图所示,某小区内有A,B,C,D四栋楼,在C栋楼处测得AC=a米,∠BAC=30°,∠BAD=90°,∠BCD=45°,∠DCA=30°.
22.如图所示,某小区内有A,B,C,D四栋楼,在C栋楼处测得AC=a米,∠BAC=30°,∠BAD=90°,∠BCD=45°,∠DCA=30°.
(1)求BD两栋楼间的距离;
(2)若小区决定沿BD方向取E,F两点与A建设一个三角形花园,且始终满足∠EAF=45°,求△AEF面积的最小值.组卷:35引用:2难度:0.5


