2022-2023学年广东省深圳市宝安区海旺中学七年级（下）期中数学试卷

一.选择题（共10题，每小题3分，共30分）

• 1．3^-2=（　　）

  A． 1 6

  B． 1 9

  C．-6

  D．-9
  组卷：256引用：5难度：0.7

  解析

• 2．下列计算中，结果正确的是（　　）

  A．a2•a3=a6	B．（a2）10=a20
  C．（2a）（3a）=6a	D．a12÷a2=a6
  组卷：290引用：5难度：0.7

  解析

• 3．华为Mate20手机搭载了全球首款7纳米制程芯片，7纳米就是0.000000007米．数据0.000000007用科学记数法表示为（　　）

  A．7×10-9

  B．0.7×10-8

  C．7×10-8

  D．7×10-7
  组卷：341引用：3难度：0.9

  解析

• 4．用一块含30°角的透明直角三角板画已知△ABC的边BC上的高，下列三角板的摆放位置正确的是（　　）

  A．

  B．

  C．

  D．
  组卷：3331引用：19难度：0.7

  解析

• 5．如图，在大烧杯中放了一个小烧杯，现向小烧杯中匀速注水，小烧杯满了后继续匀速注水，则大烧杯的液面高度h（cm）与时间注水时间t（s）的大致图象是（　　）

  A．

  B．

  C．

  D．
  组卷：2062引用：16难度：0.7

  解析

• 6．下列说法正确的有（　　）
  ①不相交的两条直线是平行线；
  ②经过直线外一点，有且只有一条直线与这条直线平行；
  ③两条直线被第三条直线所截，同旁内角互补；
  ④在同一平面内，若直线a⊥b,b⊥c,则直线a∥c.

  A．4个

  B．3个

  C．2个

  D．1个
  组卷：663引用：4难度：0.7

  解析

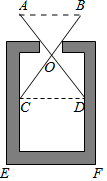• 7．在测量一个小口圆形容器的壁厚（厚度均匀）时，小明用“X型转动钳”按如图方法进行测量，其中OA=OD，OB=OC，测得AB=3厘米，EF=4厘米，圆形容器的壁厚是（　　）

  A．2厘米

  B．1.5厘米

  C．1厘米

  D．0.5厘米
  组卷：856引用：5难度：0.7

  解析

三.解答题（共7小题，共55分.）

• 21．【项目学习】配方法是数学中重要的一种思想方法，它是指将一个式子的某部分通过恒等变形化为完全平方式或几个完全平方式的和的方法，这种方法常被用到代数式的变形中，并结合非负数的意义来解决一些问题．
  例如，把二次三项式x²-2x+3进行配方
  解：x²-2x+3=x²-2x+1+2=（x²-2x+1）+2=（x-1）²+2
  我们定义：一个整数能表示成a²+b²（a,b是整数）的形式，则称这个数为“完美数”．例如，5是“完美数”，理由：因为5=2²+1²，再如，M=x²+2xy+2y²=（x+y）²+y²，（x,y是整数）所以M也是“完美数”
  【问题解决】
  （1）下列各数中，“完美数”有

  ．（填序号）
  ①10
  ②45
  ③28
  ④29
  （2）若二次三项式x²-6x+13（x是整数）是“完美数”，可配方成（x-m）²+n（m,n为常数），则mn的值为

  ；
  【问题探究】
  （3）已知S=x²+9y²+8x-12y+k（x,y是整数，k是常数），要使S为“完美数”，试求出符合条件的k的值．
  【问题拓展】
  （4）已知实数x,y满足-x²+7x+y-10=0，求x+y的最小值．
  组卷：1164引用：4难度：0.6

  解析

• 22．【问题情境】：
  课外数学兴趣小组活动时，老师提出了如下何题：
  如图①，△ABC中，若AB=10，AC=6，求BC边上的中线AD的取值范围．
  小明在组内经过合作交流，得到了如下的解决方法：延长AD至点E，使DE=AD，连接BE，请根据小明的方法思考：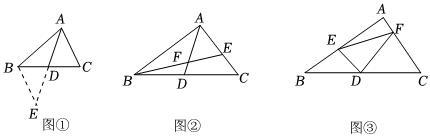
  
  （1）由已知和作图能得到△ADC≌△EDB，依据是

  ．
  A．SSS B．SAS C．AAS  D．SSA
  （2）由“三角形的三边关系”可求得AD的取值范围是

  ．
  解后反思：题目中出现“中点”、“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形之中．
  【初步运用】：
  （3）如图②，AD是△ABC的中线，BE交AC于E，交AD于F，且AE=EF．若EF=5，EC=3，求线段BF的长．
  【拓展提升】：
  （4）如图③，在△ABC中，D为BC的中点，DE⊥DF分别交AB，AC于点E，F．求证：BE+CF＞EF．
  组卷：604引用：2难度：0.1

  解析