2022-2023学年贵州省黔西南州兴仁市金成实验学校八年级（下）期末数学试卷

一.选择题（每题3分，共36分）

• 1．下列二次根式中，最简二次根式是（　　）

  A． 1 5

  B． 2

  C． 12

  D． a 2
  组卷：313引用：11难度：0.7

  解析

• 2．下列运算错误的是（　　）

  A． 2 • 3 = 6

  B． 6 ÷ 2 = 3

  C． （ - 2 2 ） 2 = 1 2

  D． 2 + 3 = 5
  组卷：24引用：2难度：0.7

  解析

• 3．若一个直角三角形的两直角边的长为12和5，则第三边的长为（　　）

  A．13或 119

  B．13或15

  C．13

  D．15
  组卷：1360引用：11难度：0.6

  解析

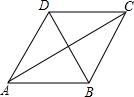• 4．如图，已知某广场菱形花坛ABCD的周长是24米，∠BAD=60°，则花坛对角线AC的长等于（　　）

  A．6 3 米

  B．6米

  C．3 3 米

  D．3米
  组卷：3109引用：83难度：0.9

  解析

• 5．如图，在Rt△ABC中，CD是斜边AB上的中线，若∠A=20°，则∠BDC=（　　）

  A．30°

  B．40°

  C．45°

  D．60°
  组卷：1428引用：22难度：0.7

  解析

• 6．一次函数y=5x-1的图象经过的象限是（　　）

  A．一、二、三

  B．一、三、四

  C．二、三、四

  D．一、二、四
  组卷：156引用：2难度：0.8

  解析

• 7．关于正比例函数y=-3x,下列结论正确的是（　　）

  A．图象不经过原点	B．y随x的增大而增大
  C．图象经过第二、四象限	D．当x= 1 3 时，y=1
  组卷：3734引用：25难度：0.7

  解析

• 8．将直线y=2x-3向右平移2个单位，再向上平移3个单位后，所得的直线的表达式为（　　）

  A．y=2x-4

  B．y=2x+4

  C．y=2x+2

  D．y=2x-2
  组卷：7771引用：40难度：0.9

  解析

三、解答题（98分）

• 24．为庆祝中华人民共和国七十周年华诞，某校举行书画大赛，准备购买甲、乙两种文具，奖励在活动中表现优秀的师生．已知购买2个甲种文具、1个乙种文具共需花费35元；购买1个甲种文具、3个乙种文具共需花费30元．
  （1）求购买一个甲种文具、一个乙种文具各需多少元？
  （2）若学校计划购买这两种文具共120个，投入资金不少于955元又不多于1000元，设购买甲种文具x个，求有多少种购买方案？
  （3）设学校投入资金W元，在（2）的条件下，哪种购买方案需要的资金最少？最少资金是多少元？
  组卷：1994引用：27难度：0.5

  解析

• 25．已知，在△ABC中，∠BAC=90°，∠ABC=45°，点D为直线BC上一动点（点D不与点B，C重合）．以AD为边作正方形ADEF，连接CF
  （1）如图1，当点D在线段BC上时．求证：CF+CD=BC；
  （2）如图2，当点D在线段BC的延长线上时，其他条件不变，请直接写出CF，BC，CD三条线段之间的关系；
  （3）如图3，当点D在线段BC的反向延长线上时，且点A，F分别在直线BC的两侧，其他条件不变；
  ①请直接写出CF，BC，CD三条线段之间的关系；
  ②若正方形ADEF的边长为2

  2

  ，对角线AE，DF相交于点O，连接OC．求OC的长度．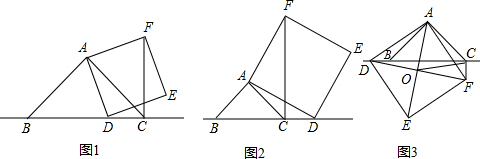
  
  组卷：3011引用：56难度：0.5

  解析