2023-2024学年浙江省金衢山五校联盟八年级(上)月考数学试卷(9月份)
发布:2024/8/28 14:0:8
一、选择题(本题有10小题,每小题3分,共30分.请选出各题中唯一的正确选项,不选、多选、错选,均不给分)
-
1.已知a,b,c是三角形的三条边,则|c-a-b|+|c+b-a|的化简结果为( )
组卷:736引用:6难度:0.6 -
2.下列命题中,是真命题的是( )
组卷:248引用:4难度:0.6 -
3.布鲁斯先生、他的妹妹、他的儿子,还有他的女儿都是网球选手.这四人中有以下情况:
①最佳选手的孪生同胞与最差选手性别不同:②最佳选手与最差选手年龄相同.则这四人中最佳选手是
( )组卷:157引用:2难度:0.5 -
4.下列图形中是轴对称图形的是( )
组卷:185引用:22难度:0.9 -
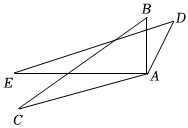 5.如图,△ABC≌△ADE,∠B=30°,∠E=20°,∠BAE=90°,则∠EAC=( )组卷:747引用:6难度:0.6
5.如图,△ABC≌△ADE,∠B=30°,∠E=20°,∠BAE=90°,则∠EAC=( )组卷:747引用:6难度:0.6 -
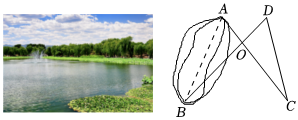 6.如图,为测量池塘两端A、B的距离,小康在池塘外一块平地上选取了一点O,连接AO,BO,并分别延长AO,BO到点C,D,使得AO=DO,BO=CO,连接CD,测得CD的长为165米,则池塘两端A,B之间的距离为( )组卷:64引用:4难度:0.7
6.如图,为测量池塘两端A、B的距离,小康在池塘外一块平地上选取了一点O,连接AO,BO,并分别延长AO,BO到点C,D,使得AO=DO,BO=CO,连接CD,测得CD的长为165米,则池塘两端A,B之间的距离为( )组卷:64引用:4难度:0.7 -
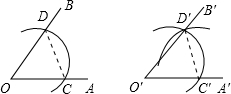 7.请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据所学的图形的全等这一章的知识,说明画出∠A′O′B′=∠AOB的依据是( )组卷:3184引用:77难度:0.9
7.请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据所学的图形的全等这一章的知识,说明画出∠A′O′B′=∠AOB的依据是( )组卷:3184引用:77难度:0.9 -
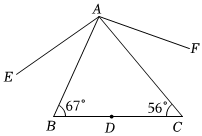 8.如图,△ABC中,D点在BC上,将D点分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF,根据图中标示的角度,∠EAF的度数为( )组卷:1041引用:7难度:0.6
8.如图,△ABC中,D点在BC上,将D点分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF,根据图中标示的角度,∠EAF的度数为( )组卷:1041引用:7难度:0.6
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
-
23.已知,AB∥CD,点E为射线FG上一点.
(1)如图1,若∠EAF=30°,∠EDG=45°,则∠AED=°;
(2)如图2,当点E在FG延长线上时,此时CD与AE交于点H,则∠AED、∠EAF、∠EDG之间满足怎样的关系,请说明你的结论:
(3)如图3,DI平分∠EDC,交AE于点K,交AI于点I,且∠EAI:∠BAI=1:2,∠AED=22°,∠I=20°求∠EKD的度数.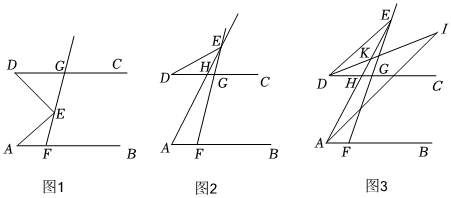 组卷:2994引用:4难度:0.1
组卷:2994引用:4难度:0.1 -
24.如图,点A,B分别在两互相垂直的直线OM,ON上.
(1)如图1,在三角形尺子ABC中,∠ABC=90°,AB=BC如果点C到直线OM的距离是5,求OB的长;
(2)如图2,若OA=6,点B在射线OM上运动时,分别以OB,AB为边作与图1中△ABC相同形状的Rt△OBF,Rt△ABE,∠ABE=∠OBF=Rt∠,连接EF交射线OM于点P.
①当∠EAO=75°时,∠EAB=45°,求∠EBP的大小;
②当点B在射线OM上移动时,PB的长度是否发生改变?若不变,求出PB的值;若变化,求PB的取值范围.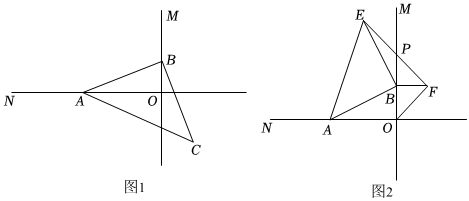 组卷:34引用:1难度:0.3
组卷:34引用:1难度:0.3


