2022-2023学年江苏省西安交大苏州附中八年级（上）段考数学试卷（10月份）

一．选择题（本大题共10小题，每小题3分，共30分）

• 1．2022年北京冬奥会会徽“冬梦”以汉字“冬”为灵感来源，运用中国书法的艺术形态，将厚重的东方文化底蕴与国际化的现代风格融为一体．以下是参选的会徽设计的一部分图形，其中是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：76引用：8难度：0.9

  解析

• 2．已知△ABC的三条边分别是a、b、c,则下列条件中不能判断△ABC是直角三角形的是（　　）

  A．a：b：c=3：4：5	B．∠C=∠A+∠B
  C．∠A：∠B：∠C=1：5：6	D．∠A：∠B：∠C=3：4：5
  组卷：440引用：6难度：0.6

  解析

• 3．下列四组数中，是勾股数的是（　　）

  A．6，8，10	B．0.3，0.4，0.5
  C． 1 3 ， 1 4 ， 1 5	D．32，42，52
  组卷：600引用：3难度：0.8

  解析

• 4．到△ABC的三边距离相等的点是△ABC的（　　）

  A．三边中线的交点	B．三条角平分线的交点
  C．三边上高的交点	D．三边垂直平分线的交点
  组卷：393引用：11难度：0.9

  解析

• 5．在直角三角形中，两条直角边长分别为5，12，则斜边上的中线长为（　　）

  A．13

  B．12

  C．6.5

  D．6
  组卷：208引用：7难度：0.8

  解析

• 6．如图，在△ABC中，AB=AC，点D为AB边上一点，且AD=CD=BC，则∠A的度数为（　　）

  A．38°

  B．36°

  C．32°

  D．30°
  组卷：705引用：4难度：0.6

  解析

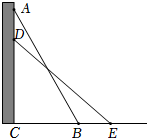• 7．如图，一架梯子AB长为5米，顶端A靠在墙AC上，这时梯子下端B与墙底端C的距离是3米，梯子下滑后停在DE的位置上，这时测得BE为1米，则梯子顶端A下滑了（　　）

  A．1米

  B．1.5米

  C．2米

  D．2.5米
  组卷：1281引用：3难度：0.6

  解析

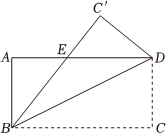• 8．如图，将长方形ABCD沿对角线BD折叠，使点C落在点C′处，BC′交AD于E，AD=8，AB=4，则重叠部分（即△BDE）的面积为（　　）

  A．6

  B．7.5

  C．10

  D．20
  组卷：1083引用：9难度：0.6

  解析

三、解答题（本大题共8小题，共54分）

• 25．【问题情境】
  课外兴趣小组活动时，老师提出了如下问题：如图1，△ABC中，若AB=12，AC=8，求BC边上的中线AD的取值范围．
  小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使DE=AD，连接BE．请根据小明的方法思考：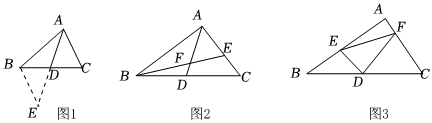
  
  （1）由已知和作图能得到△ADC≌△EDB，依据是

  ．
  A．SSS
  B．SAS
  C．AAS
  D．HL
  （2）由“三角形的三边关系”可求得AD的取值范围是

  ．
  解后反思：题目中出现“中点”“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．
  【初步运用】
  如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且AE=EF．若EF=3，EC=2，求线段BF的长．
  【灵活运用】
  如图3，在△ABC中，∠A=90°，D为BC中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF，试猜想线段BE、CF、EF三者之间的等量关系，并证明你的结论．
  组卷：283引用：4难度：0.2

  解析

• 26．【材料】在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．根据材料，解决下列问题：
  
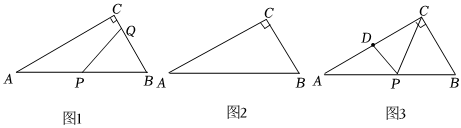
  如图1，在Rt△ABC中，∠C=90°，∠A=30°，BC=12cm.动点P从点A出发，沿射线AB运动，动点Q从点B出发，沿射线BC运动，如果动点P以2cm/s,Q以1cm/s的速度同时出发，设运动时间为t（s），解答下列问题：
  （1）当t=2时，BP=

  ；
  （2）t为多少时，△PBQ是等腰三角形？请说明理由；
  （3）P、Q在运动过程中，△PBQ的形状不断发生变化，当t为多少时，△PBQ是直角三角形？请说明理由；
  （4）如图3，取AC中点D，连接CP，DP，则CP+DP的最小值等于

  ．
  组卷：85引用：1难度：0.2

  解析