2022-2023学年安徽省阜阳市临泉一中高铁分校高二（下）第三次月考数学试卷
发布：2024/5/18 8:0:8
一、单选题（本大题共8小题，共40分．）
-
1．已知随机变量X～N（2，σ2），P（X≤4）=0.8，那么P（2≤X≤4）的值为（ ）
组卷：268引用：5难度：0.9 -
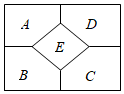2．如图所示的五个区域中，中心区域是一幅图画，现要求在其余四个区域中涂色，有四种颜色可供选择．要求每个区域只涂一种颜色，相邻区域所涂颜色不同，则不同的涂色方法种数为（ ）组卷：636引用：14难度：0.9 -
3．利用独立性检验考察两个变量X与Y是否有关系，通过2×2列联表进行独立性检验．经计算χ2=4.964，那么认为X与Y是有关系，这个结论错误的可能性不超过（ ）
P（K2≥k0） 0.100 0.050 0.025 0.010 0.001 k0 2.706 3.841 5.024 6.635 10.828 组卷：43引用：1难度：0.7 -
4．变量x,y具有线性相关关系，根据下表数据，利用最小二乘法可以得到其回归直线方程
，则̂y=10.5x+̂a=（ ）̂ax 2 4 5 6 8 y 20 40 60 70 80 组卷：64引用：3难度：0.7 -
5．为了应对即将到来的汛期，某地防汛指挥部抽调6名专业人员（包括甲、乙两人）平均分成三组，对当地三处重点水利工程进行防汛安全检查，则甲、乙不同组的概率为（ ）
组卷：74引用：5难度：0.7 -
6．从装有6个白球，2个红球的密闭容器中逐个不放回地摸取小球．若每取出1个红球得2分，每取出1个白球得1分．按照规则从容器中任意抽取2个球，所得分数的期望为（ ）
组卷：228引用：5难度：0.5 -
7．如图是一块高尔顿板示意图：在一块木块上钉着若干排互相平行但相互错开的圆柱形小木钉，小木钉之间留有适当的空隙作为通道，前面挡有一块玻璃，将小球从顶端放入，小球在下落过程中，每次碰到小木钉后都等可能地向左或向右落下，最后落入底部的格子中，格子从左到右分别编号为0，1，2，3，4，5用X表示小球落入格子的号码，则下面计算错误的是（ ）组卷：187引用：4难度：0.5
四、解答题（本大题共6小题，共70分．）
-
21．“城市公交”泛指城市范围内定线运营的公共汽车及轨道交通等交通方式，也是人们日常出行的主要方式．某城市的公交公司为了方便市民出行，科学规划车辆投放，在一个人员密集流动地段增设一个起点站，为了研究车辆发车间隔时间x与乘客等候人数y之间的关系，经过调查得到如下数据：
（1）根据以上数据作出折线图，易知可用线性回归模型拟合y与x的关系，请用相关系数加以说明；间隔时间（x分钟） 6 8 10 12 14 等候人数（y人） 15 18 20 24 23
（2）建立y关于x的回归直线方程，并预测车辆发车间隔时间为20分钟时乘客的等候人数．
附：对于一组数据（x1，y1），（x2，y2），…（xn，yn），其回归直线的斜率和截距的最小二乘估计分别为̂y=̂bx+̂a，̂b=n∑i=1xiyi-nxyn∑i=1x2i-nx2=n∑i=1（xi-x）（yi-y）n∑i=1（xi-x）2；相关系数̂a=y-̂bx；r=n∑i=1（xi-x）（yi-y）n∑i=1（xi-x）2n∑i=1（yi-y）2．315≈11.62组卷：149引用：6难度：0.5 -
22．某商店计划七月份订购某种饮品，进货成本为每瓶2元，未售出的饮品降价处理，以每瓶1元的价格当天全部处理完．依经验，零售价与日需求量依据当天的温度而定，当气温T≥35℃时，零售价为每瓶5元，日需求量为300瓶；当30℃≤T＜35℃时，零售价为每瓶4元，日需求量为200瓶；当T＜30℃时，零售价为每瓶3元，日需求量为100瓶．已知七月份每天气温T≥35℃的概率为0.6，30℃≤T＜35℃的概率为0.2，T＜30℃的概率为0.2．
（1）求七月份这种饮品一天的平均需求量；
（2）若七月份某连续三天每天的气温均不低于30℃，求这三天销售这种饮品的总利润的分布列及数学期望．组卷：74引用：1难度：0.2
