2023年山东省东营一中高考数学二模试卷

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知复数z是一元二次方程x²-2x+2=0的一个根，则|z|的值为（　　）

  A．1

  B． 2

  C．0

  D．2
  组卷：487引用：11难度：0.9

  解析

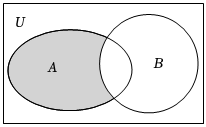• 2．已知全集U=R，集合A={x|log₂x≤2}，B={x|1＜x＜5}，则图中阴影部分表示的集合为（　　）

  A．{x|x≤5}

  B．{x|0＜x≤1}

  C．{x|x≤4}

  D．{x|1＜x≤5}
  组卷：215引用：7难度：0.8

  解析

• 3．已知m,n表示空间内两条不同的直线，则使m∥n成立的必要不充分条件是（　　）

  A．存在平面α，有m∥α，n∥α	B．存在平面α，有m⊥α，n⊥α
  C．存在直线l,有m⊥l,n∥l	D．存在直线l,有m∥l,n∥l
  组卷：120引用：6难度：0.7

  解析

• 4．为了激发同学们学习数学的热情，某学校开展利用数学知识设计LOGO的比赛，其中某位同学利用函数图像的一部分设计了如图的LOGO，那么该同学所选的函数最有可能是（　　）

  A．f（x）=x-sinx	B．f（x）=sinx-xcosx
  C． f （ x ） = x 2 - 1 x 2	D．f（x）=sinx+x3
  组卷：249引用：10难度：0.6

  解析

• 5．已知3^a=5^b=15，则下列结论正确的是（　　）

  A．a＜b	B．（a-1）2+（b-1）2＞2
  C．ab＞5	D．a2+b2＜8
  组卷：234引用：4难度：0.6

  解析

• 6．传说国际象棋发明于古印度，为了奖赏发明者，古印度国王让发明者自己提出要求，发明者希望国王让人在他发明的国际象棋棋盘上放些麦粒，规则为：第一个格子放一粒，第二个格子放两粒，第三个格子放四粒，第四个格子放八粒…依此规律，放满棋盘的64个格子所需小麦的总重量大约为（　　）吨．（1kg麦子大约20000粒，lg2=0.3）

  A．105

  B．107

  C．1012

  D．1015
  组卷：200引用：5难度：0.6

  解析

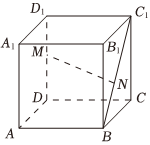• 7．在正方体ABCD-A₁B₁C₁D₁中，点M，N分别是棱DD₁和线段BC₁上的动点，则满足与DD₁垂直的直线MN（　　）

  A．有且仅有1条	B．有且仅有2条
  C．有且仅有3条	D．有无数条
  组卷：569引用：4难度：0.7

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．已知椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左、右焦点分别为F₁，F₂，P是C上异于左、右顶点的动点，

  P

  F

  1

  •

  P

  F

  2

  的最小值为2，且C的离心率为

  1

  2

  ．
  （1）求椭圆C的方程．
  （2）若圆E与△PF₁F₂的三边都相切，判断是否存在定点M，N，使|EM|+|EN|为定值．若存在，求出点M，N的坐标；若不存在，请说明理由．
  组卷：112引用：3难度：0.5

  解析

• 22．已知函数f（x）=

  2

  x

  x

  +

  1

  ，g（x）=

  sinx

  x

  ．
  （1）求f（x）的单调区间；
  （2）证明：-

  1

  4

  ＜g（x）＜1；
  （3）设x₁=

  2

  ，x_n+1=f（x_n），证明：x₁x₂…x_n＜

  π

  2

  ．
  组卷：122引用：3难度：0.5

  解析