2022-2023学年天津市重点校联考高一(下)期末数学试卷
发布:2024/6/16 8:0:10
一、选择题(本题共8小题,每小题4分,共32分)
-
1.已知(1+i)z=3+i,其中i为虚数单位,则|z|=( )
组卷:107引用:2难度:0.8 -
2.已知向量
=(-1,2),a=(1,1),则b在a上的投影向量为( )b组卷:503引用:6难度:0.8 -
3.已知三条不同的直线l,m,n和两个不同的平面α,β,下列四个命题中正确的为( )
组卷:919引用:11难度:0.6 -
4.已知△ABC中,角A,B,C所对的边分别是a,b,c,若(a+b-c)(b+c+a)=3ab,且sinC=2sinBcosA,那么△ABC是( )
组卷:136引用:2难度:0.7 -
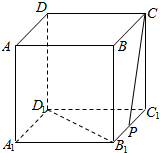
5.在棱长为1的正方体ABCD-A1B1C1D1中,P为B1C1的中点,那么直线CP与B1D1所成角的余弦值是( )
 组卷:650引用:7难度:0.9
组卷:650引用:7难度:0.9 -
6.盒中装有形状、大小完全相同的4个球,其中红色球2个,黄色球2个.若从中随机取出2个球,则所取出的2个球颜色相同的概率等于( )
组卷:222引用:1难度:0.8
三、解答题(本大题共5小题,共64分)
-
18.已知△ABC内角A,B,C的对边分别为a,b,c,且3a+2b=3ccosB.
(1)求cosC的值;
(2)若,求△ABC的面积.c=31,a+b=6组卷:103引用:2难度:0.5 -
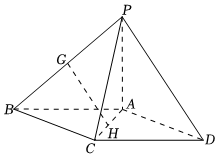 19.如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,△PCD为等边三角形,平面PAC⊥平面PCD,PA⊥CD,CD=4,AD=6.
19.如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,△PCD为等边三角形,平面PAC⊥平面PCD,PA⊥CD,CD=4,AD=6.
(1)设G,H分别为PB,AC的中点,求证:GH∥平面PAD;
(2)求证:PA⊥平面PCD;
(3)求直线AD与平面PAC所成角的正弦值.组卷:532引用:4难度:0.5


