2022-2023学年山西省朔州市怀仁市高二（下）期末数学试卷

一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合要求的

• 1．某兴趣小组研究光照时长x（h）和向日葵种子发芽数量y（颗）之间的关系，采集5组数据，作如图所示的散点图．若去掉D（10，2）后，下列说法正确的是（　　）

  A．相关系数r变小

  B．决定系数R2变小

  C．残差平方和变大

  D．解释变量x与预报变量y的相关性变强
  组卷：294引用：10难度：0.7

  解析

• 2．已知等差数列{a_n}的前n项和S_n，若a₂+a₃+a₁₄+a₁₅=40，则S₁₆=（　　）

  A．150

  B．160

  C．170

  D．180
  组卷：311引用：5难度：0.8

  解析

• 3．已知随机变量服X从正态分布N（2，σ²），且

  P

  （

  X

  ＞

  3

  ）

  =

  1

  6

  ，则P（1≤X＜2）=（　　）

  A． 1 3

  B． 1 6

  C． 2 3

  D． 5 6
  组卷：19引用：2难度：0.7

  解析

• 4．已知在15个村庄中有7个村庄交通不方便，现从中任意选10个村庄，用X表示10个村庄中交通不方便的村庄数，则下列概率中等于

  C

  4

  7

  C

  6

  8

  C

  10

  15

  的是（　　）

  A．P（X=2）

  B．P（X≤2）

  C．P（X=4）

  D．P（X≤4）
  组卷：27引用：2难度：0.7

  解析

• 5．一组数据按照从小到大的顺序排列为1，2，3，5，6，8，记这组数据的上四分位数为n,则二项式

  （

  2

  x

  -

  1

  x

  ）

  n

  展开式的常数项为（　　）

  A．-160

  B．60

  C．120

  D．240
  组卷：292引用：5难度：0.7

  解析

• 6．某校得到北京大学给的10个推荐名额，现准备将这10个推荐名额分配给高三年级的6个班级（每班至少一个名额），则高三（1）班恰好分到3个名额的概率为（　　）

  A． 1 10

  B． 5 42

  C． 1 6

  D． 35 126
  组卷：113引用：2难度：0.7

  解析

• 7．某同学在研究性学习中，收集到某制药厂今年前5个月甲胶囊生产产量（单位：万盒）的数据如表所示：
  

  x（月份）	1	2	3	4	5
  y（万盒）	5	5	6	6	8

  若x,y线性相关，线性回归方程为

  ̂

  y

  =0.7x+

  ̂

  a

  ，则以下判断正确的是（　　）

  A．x每增加1个单位长度，则y 一定增加0.7个单位长度

  B．x每减少1个单位长度，则y必减少0.7个单位长度

  C．当x=6时，y的预测值为8.1万盒

  D．线性回归直线 ̂ y =0.7x+ ̂ a 经过点（2，6）
  组卷：196引用：7难度：0.7

  解析

四、解答题：本大题共6小题，共70分，其中第17题10分，其它每题12分，解答应写出文字说明、证明过程或演算步骤．

• 21．某市举行招聘考试，共有4000人参加，分为初试和复试，初试通过后参加复试．为了解考生的考试情况，随机抽取了100名考生的初试成绩，并以此为样本绘制了样本频率分布直方图，如图所示．
  
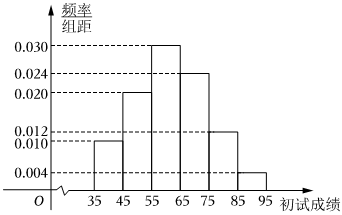
  （1）根据频率分布直方图，试求样本平均数的估计值；
  （2）若所有考生的初试成绩X近似服从正态分布N（μ，σ²），其中μ为样本平均数的估计值，σ≈13，试估计初试成绩不低于88分的人数；
  （3）复试共三道题，第一题考生答对得5分，答错得0分，后两题考生每答对一道题得10分，答错得0分，答完三道题后的得分之和为考生的复试成绩．已知某考生进入复试，他在复试中第一题答对的概率为

  3

  4

  ，后两题答对的概率均为

  3

  5

  ，且每道题回答正确与否互不影响．记该考生的复试成绩为Y，求Y的分布列及均值．
  附：若随机变量X服从正态分布N（μ，σ²），则：P（μ-σ＜X＜μ+σ）=0.6827，P（μ-2σ＜X＜μ+2σ）=0.9545，P（μ-3σ＜X＜μ+3σ）=0.9973．
  组卷：339引用：7难度：0.6

  解析

• 22．已知函数f（x）=e^x+acosx.
  （1）若函数f（x）在区间

  （

  0

  ，

  π

  2

  ）

  上恰有两个极值点，求a的取值范围；
  （2）证明：当

  1

  ≤

  a

  ≤

  e

  π

  2

  -

  2

  -

  π

  2

  时，在（0，+∞）上，f（x）＞2+x恒成立．
  组卷：56引用：4难度：0.3

  解析