菁于教，优于学

申请校本题库

试卷征集

加入会员

操作视频

当前位置：试卷中心 > 试卷详情

2022-2023学年辽宁省大连育明高级中学高一（下）第一次段考数学试卷

发布：2024/5/16 8:0:9

一、单选题

1．若角θ的终边经过点（-2，3），则sin（π+θ）=（　　）
A．
-
3
13
13
B．
-
2
13
13
C．
2
13
13
D．
3
13
13
组卷：395引用：6难度：0.8
解析
2．下列四个函数中，以π为最小正周期，且在区间（
π
2
，π）上单调递减的是（　　）
A．y=sinx B．y=|sinx| C．y=cosx D．y=tanx
组卷：282引用：6难度：0.7
解析
3．已知|
a
|=
2
，|
b
|=1，
a
与
b
的夹角为
π
4
，则|
a
+2
b
|=（　　）
A．8 B．10 C．
10
D．2
2
组卷：1021引用：3难度：0.7
解析
4．已知θ是第三象限角，且sin⁴θ+cos⁴θ=
5
9
，则sinθcosθ的值为（　　）
A．
2
3
B．-
2
3
C．
1
3
D．-
1
3
组卷：244引用：1难度：0.7
解析
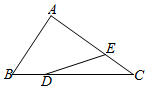5．如图，△ABC中，
AB
=
a
，
AC
=
b
，
DC
=3
BD
，
AE
=2
EC
，则
DE
等于（　　）
A．
-
1
3
a
+
3
4
b
B．
5
12
a
-
3
4
b
C．
3
4
a
+
1
3
b
D．
-
3
4
a
+
5
12
b
组卷：811引用：8难度：0.5
解析
6．如图是函数f（x）=cos（πx+φ）（0＜φ＜
π
2
）的部分图象，则f（3x₀）=（　　）
A．
1
2
B．-
1
2
C．
3
2
D．-
3
2
组卷：364引用：2难度：0.7
解析
7．已知点P是△ABC的内心（三个内角平分线交点）、外心（三条边的中垂线交点）、重心（三条中线交点）、垂心（三个高的交点）之一，且满足2
AP
•
BC
=
AC
2
-
AB
2
，则点P一定是△ABC的（　　）
A．内心 B．外心 C．重心 D．垂心
组卷：317引用：6难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题

21．已知函数
f
（
x
）
=
2
sin
（
x
+
π
3
）
．
（1）若不等式|f（x）-m|≤3对任意
x
∈
[
-
π
6
，
π
3
]
恒成立，求整数m的最大值；
（2）若函数
g
（
x
）
=
f
（
π
2
-
x
）
，将函数g（x）的图像上各点的横坐标缩短到原来的
1
2
倍（纵坐标不变），再向右平移
π
12
个单位，得到函数y=h（x）的图像，若关于x的方程
1
2
h
（
x
）
-
k
（
sinx
+
cosx
）
=
0
在
x
∈
[
-
π
12
，
5
π
12
]
上有解，求实数k的取值范围．
（参考公式：sin2x=2sinxcosx,
sinx
+
cosx
=
2
sin
（
x
+
π
4
）
）
组卷：229引用：3难度：0.5
解析
22．在平面直角坐标系中，O为坐标原点，A，B，C三点满足
OC
=
1
3
OA
+
2
3
OB
．
（1）求|
AC
CB
|的值；
（2）已知A（1，cosx），B（1+cosx,cosx），x∈[0，
π
2
]，f（x）=
OA
•
OC
-（2m+
2
3
）|
AB
|，若f（x）的最小值为g（m），求g（m）的最大值．
组卷：411引用：7难度：0.3
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

商务合作服务条款走进菁优

帮助中心兼职招聘意见反馈

深圳市菁优智慧教育股份有限公司

粤ICP备10006842号公网安备44030502001846号

©2010-2025 jyeoo.com 版权所有

深圳市市场监管
主体身份认证

APP开发者：深圳市菁优智慧教育股份有限公司| 应用名称：菁优网 | 应用版本：5.0.7 |隐私协议|第三方SDK|用户服务条款

广播电视节目制作经营许可证|出版物经营许可证|网站地图

本网部分资源来源于会员上传，除本网组织的资源外，版权归原作者所有，如有侵犯版权，请立刻和本网联系并提供证据，本网将在三个工作日内改正