2023年海南省海口市中考数学二模试卷
发布:2024/6/11 8:0:9
一、选择题(本大题满分36分,每小题3分)
-
1.|-3|的相反数是( )
组卷:325引用:1难度:0.8 -
2.数据160000000用科学记数法表示为( )
组卷:51引用:7难度:0.9 -
3.计算(2ab)2÷ab2,正确的结果是( )
组卷:122引用:1难度:0.7 -
4.若x-3y=4,则3-2x+6y的值是( )
组卷:312引用:1难度:0.7 -
5.下面有4组立体图形,从左面看与其他3组不同的是( )
组卷:183引用:5难度:0.7 -
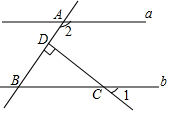 6.如图,直线a∥b,CD⊥AB于点D,若∠1=36°,则∠2等于( )组卷:161引用:3难度:0.7
6.如图,直线a∥b,CD⊥AB于点D,若∠1=36°,则∠2等于( )组卷:161引用:3难度:0.7 -
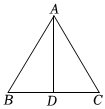 7.如图,在△ABC中,AB=AC=10,BC=12,AD平分∠BAC,则AD等于( )组卷:1931引用:9难度:0.7
7.如图,在△ABC中,AB=AC=10,BC=12,AD平分∠BAC,则AD等于( )组卷:1931引用:9难度:0.7
三、解答题(本大题满分72分)
-
21.(1)【证明推断】如图1,在正方形ABCD中,点E是对角线BD上的动点(与点B、D不重合),连接AE,过点E作EF⊥AE,EG⊥BD,分别交直线BC于点F、G.
①求证:△ABE≌△FGE;
②求的值;EFAE
(2)【类比探究】如图2,将(1)中的“正方形ABCD”改为“矩形ABCD”,其他条件均不变.
①若AB=3,BC=4,求的值;EFAE
②若AB=m•BC,直接写出的值(用含m的代数式表示);EFAE
(3)【拓展运用】如图3,在矩形ABCD中,点E是对角线BD上一点(与点B、D不重合),连接AE,过点E作EF⊥AE,EG⊥BD,分别交直线BC于点F、G,连接CE,当AB=2,BC=4,CE=CD时,求EF的长.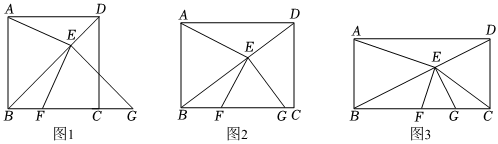 组卷:241引用:1难度:0.2
组卷:241引用:1难度:0.2 -
22.在平面直角坐标系中,把抛物线
向右平移2个单位,再向上平移y1=-12x2个单位后得到的新抛物线为y2=ax2+bx+c(a≠0),新抛物线的顶点为D,对称轴与原抛物线交于点E.92
(1)写出新抛物线的解析式,及其与x轴的两个交点A、B的坐标;
(2)点P是新抛物线上位于对称轴右侧的一个动点,设点P的横坐标为t.
①如图1,过点P作PF⊥DE于点F,当2<t<5时,求PF+FE的最大值;
②如图2,连接AE、PE,当∠PEA=90°时,求点P的横坐标;
③若点Q是x轴上一点,求使以点A、E、P、Q为顶点的四边形是平行四边形时点P的横坐标.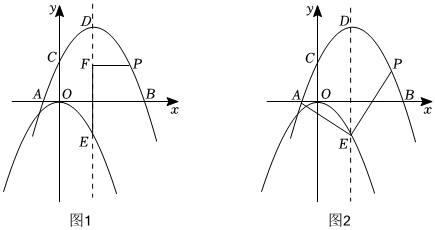 组卷:99引用:1难度:0.2
组卷:99引用:1难度:0.2


